Void Fraction#

In this subsection, all parameters required for the calculation of the void fraction are introduced.

subsection void fraction
  set mode                       = pcm
  set read dem                   = true
  set dem file name              = dem
  set l2 smoothing length        = 0
  set particle refinement factor = 0
end

  • The mode parameter allows the user to choose the method for void fraction calculation. Currently, there are two methods implemented. The first one is to calculate the void fraction from function. In this case, an additional subsection is required to insert the function such as:

# in the void fraction subsection
subsection function
set Function expression = 0.5 + 0.25*sin(pi*x)*sin(pi*y)
end

If the mode chosen is pcm, then the void fraction is calculated using the Particle Centered Method. If it is set to qcm, then the void fraction is calculated using the Quadrature Centered Method. If it is set to spm, then the void fraction is calculated using the satellite point method (divided approach). In these methods, the remaining parameters are required:

# in the void fraction subsection
set qcm sphere diameter          = 0
set qcm sphere equal cell volume = false
set particle refinement factor   = 0
set quadrature rule              = gauss
set n quadrature points          = 0

  • The read dem allows us to read an already existing dem simulation result which can be obtained from checkpointing the Lethe-DEM simulation. This is important as the lethe-fluid-vans solver requires reading an initial dem triangulation and particle information to simulate flows in the presence of particles.

  • The dem_file_name parameter specifies the prefix of the dem files that must be read.

  • The l2 smoothing length is a smoothing length used for smoothing the L2 projection of the void fraction to avoid sharp discontinuities which can lead to instabilities in the simulation.

  • The qcm sphere diameter allows us to fix the diameter of all reference spheres in the simulation to a given value. If this option is used (a value other than 0 is specified), it overrides the default calculation of the size of the sphere and sets its diameter to the value specified.

  • The qcm sphere equal cell volume determines whether or not we want to use a reference sphere with the same volume as the element in which it is located. If it is disabled, then each sphere will have a radius equal to the size of the element in which it is located. This parameter is important only when the qcm sphere diameter is not used or is set to 0.

  • The quadrature rule is only required for the qcm. The parameter allows us to choose the quadrature rule for the calculation of the void fraction. Such quadrature rule dictates the position of the quadrature points in the void fraction calculation. Currently, the implemented quadrature rules are Gauss (gauss) and Gauss-Lobatto (gauss-lobatto). The default behavior is set quadrature rule = gauss.

  • The n quadrature points is only required for the qcm. The parameter allows us to specify the number of quadrature points to be used in the void fraction calculation. If the number of quadrature points is not specified or it is set to 0, the default value will be void_fraction_degree + 1 (in general 2) for the case of Gauss quadrature rule and void_fraction_degree+2 (in general 3) for the case of Gauss-Lobatto quadrature rule.

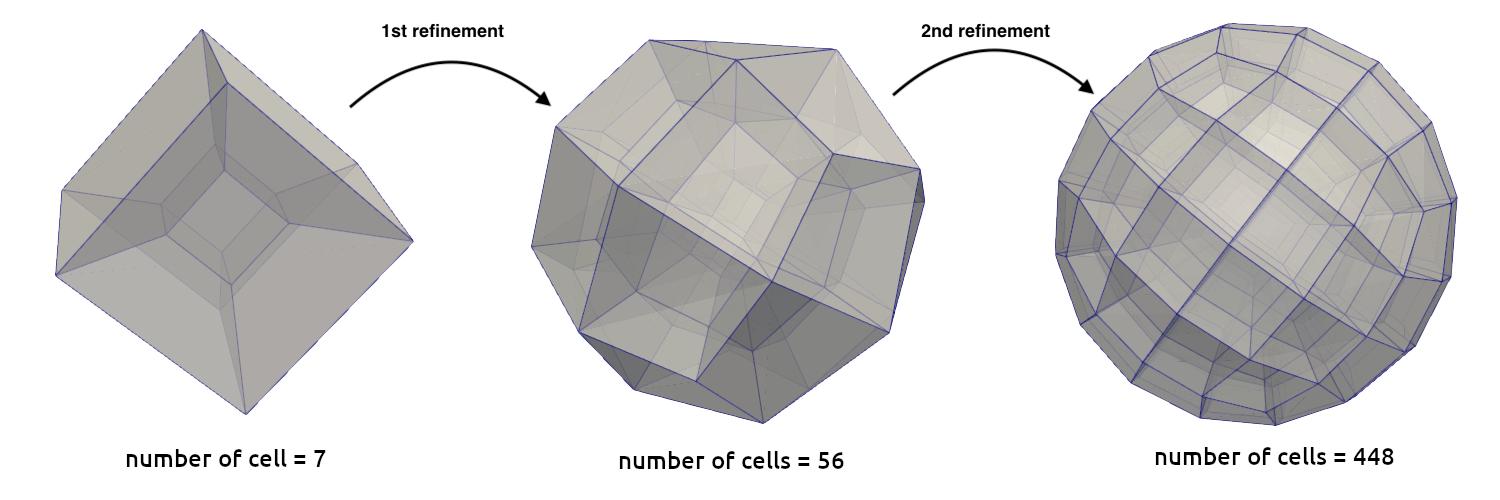
  • The particle refinement factor is only required for the spm. It allows to determine the number of pseudo-particles that we want to divide our particle into. By default, it is set to 0 refinements, and results in no refinement of the original meshed particle (division into 7 particles in 3D). Every additional refinement results in a \(2^{dim}\) times more particles. The figure below shows how the number of pseudo-particles change with every refinement. Every cell in the particle mesh represents a pseudo-particle in the satellite point method.

../../_images/refinement1.png