Granular Dam-Break#
This example simulates the dam-break flow of a dry granular material using the discrete element method (DEM). More information regarding the DEM parameters are given in the Lethe documentation, i.e. DEM parameters.
Features#
Solvers:
lethe-particlesThree-dimensional problem
Moving floating mesh
Load-balancing
Files Used in This Example#
All files mentioned below are located in the example’s folder (examples/dem/3d-dam-break).
Geometry file:
square.geoMesh file:
square.mshParameters file for the problem (\(H=20 \, \text{cm}\)):
granular-dam-break.prmParameters file for the \(H=40 \, \text{cm}\) bed:
granular-dam-break-H-40cm.prm
Description of the Case#
This example simulates the dam-break flow of a dry powder. First, a packing of particles is generated by inserting particles behind a sluice gate. After 0.5s, the sluice gate rises and the particles are able to flow freely, producing a dam-break flow. We compare the results we obtain with those of Evangelista et al. [1] To ensure that the simulation remains computationally efficient, we will scale-up the sand particles used by Evangelista et al. from a diameter of 1.6mm to 10mm. This reduces their number by a factor of approximately 250x. We first simulate case B1 of Evangelista et al., with a bed length of 60cm and bed height of 20cm. As an extension, we also simulate a bed height of 40cm (case B3).
Parameter File#
Mesh#
The domain we simulate is a rectangular box which is \(2\times0.4\times0.4\) meters and is made using the deal.ii grid generator. The grid is refined 4 times using the set initial refinement parameter.
subsection mesh
set type = dealii
set grid type = subdivided_hyper_rectangle
set grid arguments = 5,1,1 : 0,0,0 : 2,0.4,0.4 : false
set initial refinement = 4
end
Lagrangian Physical Properties#
The particles are mono dispersed with a radius of 0.005 m and a density of 2560 \(kg/m^3\), respectively. We insert 60k particles to ensure an initial height of 0.2m in order to match the B1 experiment of Evangelista et al.. The friction coefficient and the rolling coefficient are the most important parameters in this simulation, since they control the final repose angle of the particles as well as the speed of the progression of the dam-break flow. Since sand is generally non-spherical, we choose relatively high values for the friction and the rolling friction coefficients.
subsection lagrangian physical properties
set g = 0, -9.81, 0.0
set number of particle types = 1
subsection particle type 0
set size distribution type = uniform
set diameter = 0.01
set number of particles = 60000
set density particles = 2560
set young modulus particles = 1e6
set poisson ratio particles = 0.2
set restitution coefficient particles = 0.9
set friction coefficient particles = 0.5
set rolling friction particles = 0.3
end
set young modulus wall = 1e6
set poisson ratio wall = 0.2
set restitution coefficient wall = 0.9
set friction coefficient wall = 0.5
set rolling friction wall = 0.3
end
Model Parameters#
In this example, we use the frequent load balancing method to ensure that the division of the domain amongst the various processing cores follow the particles.
subsection model parameters
subsection contact detection
set contact detection method = dynamic
set dynamic contact search size coefficient = 0.9
end
subsection load balancing
set load balance method = frequent
set frequency = 5000
set threshold = 1.3
end
set particle particle contact force method = hertz_mindlin_limit_overlap
set rolling resistance torque method = constant
set particle wall contact force method = nonlinear
set integration method = velocity_verlet
end
Particle Insertion#
An insertion box is defined inside the rectangular box. 60 000 particles are inserted behind the sluice gate which is located at \(x=0.6\). It is important to note the size of the insertion box to make sure it is completely inside our geometry. Otherwise, particles will be lost during the insertion stage.
subsection insertion info
set insertion method = volume
set inserted number of particles at each time step = 60000
set insertion frequency = 10000
set insertion box points coordinates = 0.0025, 0.0025, 0.0025 : 0.597, 0.340, 0.397
set insertion distance threshold = 1.075
set insertion maximum offset = 0.025
set insertion prn seed = 19
end
Moving Solid Object#
The sluice gate which prevents the particle from floating is made of a 3D surface mesh of a flat wall. This is handled using the solid objects parameters. We insert one solid object which is generated using GMSH. To parametrize the motion of the sluice gate, we set its translational velocity to \(\mathbf{v}=[0,1,0]^T \forall t \in [0.5,0.7]s\) and we keep it static otherwise. This ensures that the sluice gate moves upward between 0.5 and 0.7s and stops moving afterwards. To ensure maximal computational efficiency, it is important to minimize the number of triangles used in the surface meshes that represent moving objects.
subsection solid objects
subsection solid surfaces
set number of solids = 1
subsection solid object 0
subsection mesh
set type = gmsh
set file name = square.msh
set simplex = true
set initial refinement = 0
end
subsection translational velocity
set Function expression = 0 ; if(t>0.5,if(t<0.7,1,0),0) ; 0
end
subsection angular velocity
set Function expression = 0 ; 0 ; 0
end
end
end
end
Simulation Control#
The simulation runs for 2 seconds of real time. We output the simulation results every 500 iterations.
subsection simulation control
set time step = 5e-5
set time end = 2
set log frequency = 500
set output frequency = 500
set output path = ./output/
set output boundaries = true
end
Running the Simulation#
The simulation is launched using a single input file for the insertion of the particles, the opening of the sluice gate and the granular motion of the particles.
Note
This example needs a simulation time of approximately 10 minutes on 8 processors using an 12th Gen Intel(R) Core(TM) i9-12900K.
Results#
Results for \(H=20 \ \text{cm}\)#
The following movie displays the dam-break flow:
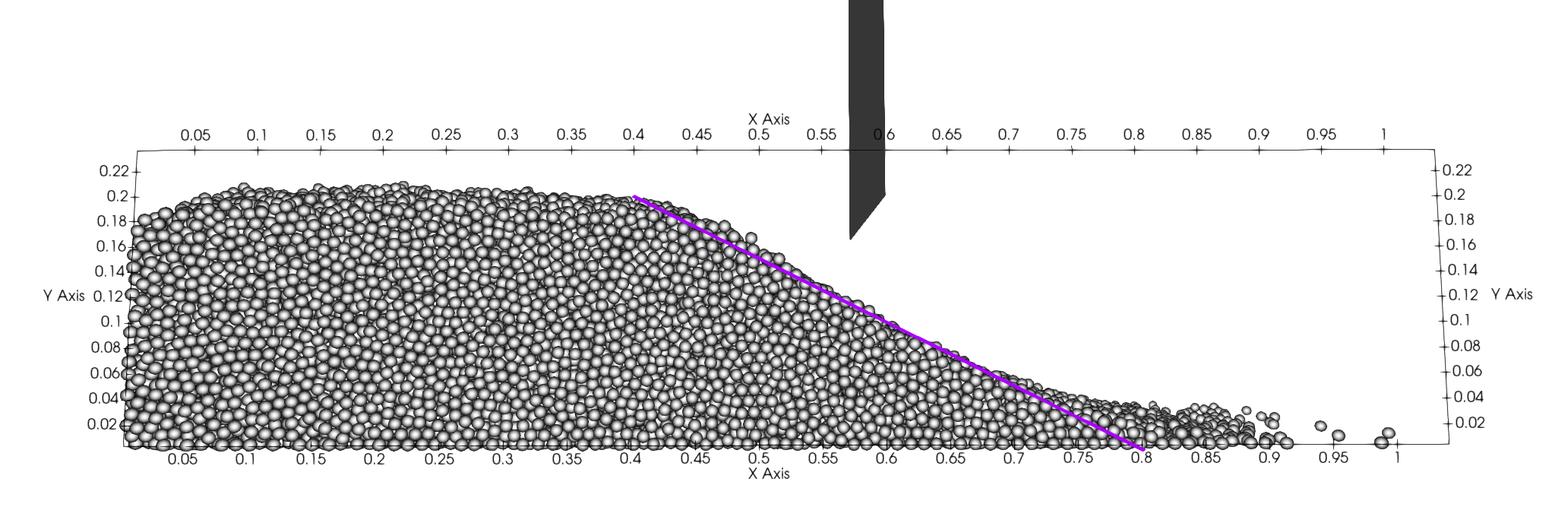
The following image compares the final repose angle of the particles with the results of Evangelista et al. We note the good agreement between the two. Evangelista et al. also found experimentally that the particle height profile varied from \(0.2m\) at \(x=0.4m\) to \(\approx 0.025m\) at \(x=0.8m\) which is in good agreement with what we observe here.
Results for \(H=40 \ \text{cm}\)#
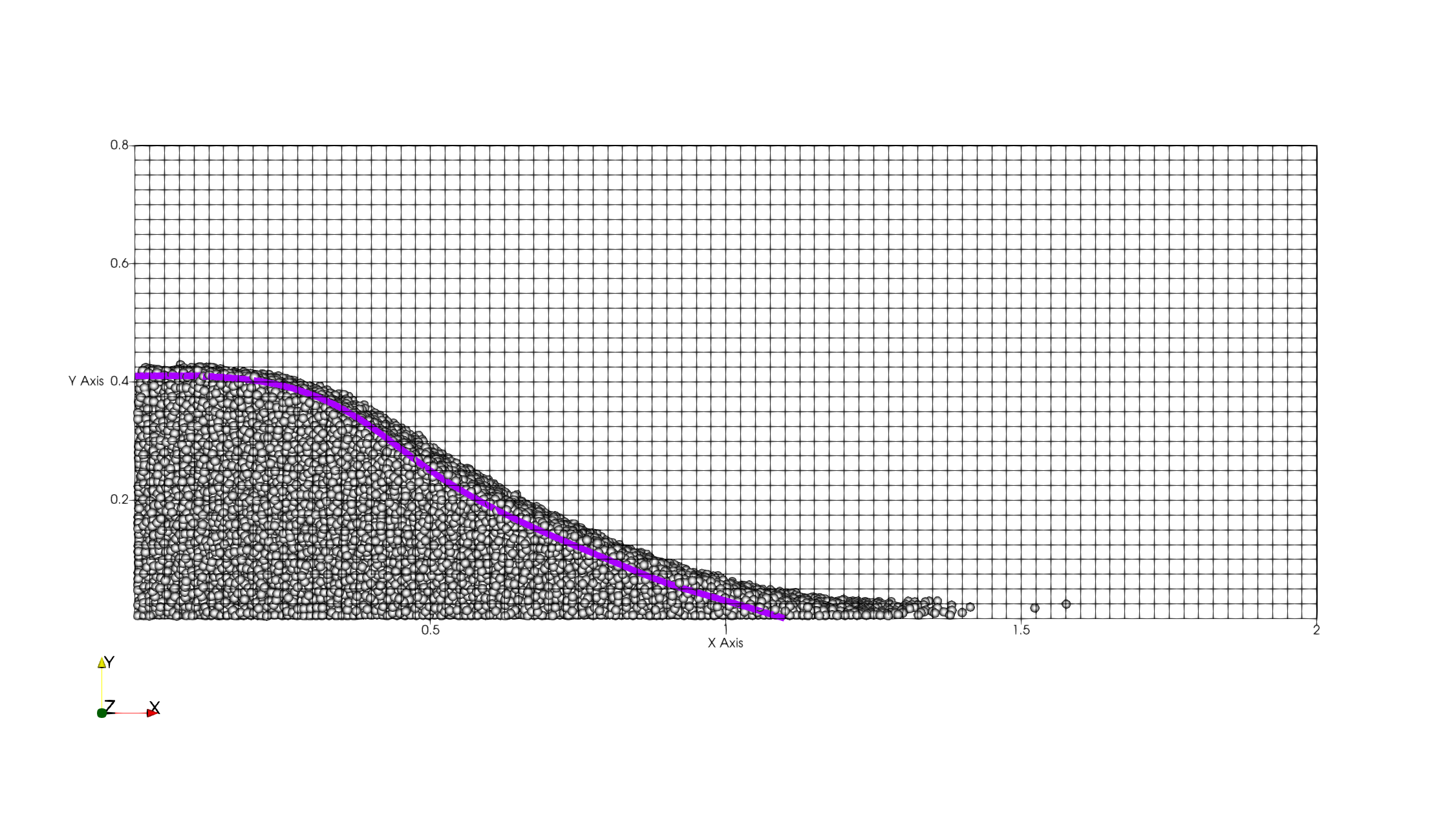
The following image compares the final granular profile of the particles with the results of Evangelista et al (illustrated using a magenta curve). We note the good agreement between the two, except for the fact that a few particles have moved further away (\(x>1.1m\)) than the one from the experiments of Evangelista et al. This is a consequence of the fact that we have used larger particles to simulate the case.
Possibilities for Extension#
Study the impact of the friction and rolling friction coefficients on the dam-break flow.
Change the height of the bed to 30cm or 50m and try to reproduce the other experiments of Evangelista et al.
Use smaller particles and reproduce the full experiment of Evangelista et al.