Sedimentation of One Particle

This example aims to numerically reproduce the results obtained by Ten Cate et al. [1] for the E4 experience. This experience measures the velocity of the sedimentation of a 1.5 cm particle in a container filled with a viscous fluid. The container is sufficiently small to impact the particle sedimentation.

Warning

• This case is a computationally expensive example. It can take several hours to run on a desktop computer.

Features

• Solvers: lethe-fluid-sharp (with Q1-Q1)

• Transient problem

• Displays the capability of the resolved CFD-DEM solver for the flow around one particle

Files Used in This Example

• Parameter file: /examples/sharp-immersed-boundary/sedimentation-1-particle/sedimentation-1-particle.prm

Description of the Case

The E4 experiment consists of the release of a particle made of Nylon (\(\rho_p=0.001120 \frac{\text{kg}}{\text{cm}^{3}}\)) with a diameter of 1.5cm. The center of the particle is located 12.75 cm above the bottom of a 10x16x10 cm container. The viscosity of the fluid is \(\mu_f=0.00058 \frac{\text{kg}}{\text{s cm}}\) which is equivalent to \(\mu_f=0.058 \frac{\text{N s}}{\text{m}^{2}}\). The density of the fluid is \(\rho_f=0.000960 \frac{\text{kg}}{\text{cm}^{3}}\). The gravity constant is \(g= -981 \frac{\text{cm}}{\text{s}^{2}}\). The particle accelerates due to gravity until it hits the bottom of the container, at which point we stop the simulation.

Note

You will note that we have transformed every length unit into centimeters. The reason is that the particle’s size is very close to 1 cm. Representing the problem in this way helps the linear solver converge. It avoids extremely small values in the matrix due to the volume of cells being expressed in \(\text{cm}^{3}\) instead of \(\text{m}^{3}\).

All the container walls have no-slip boundary conditions except at the top of the container, where we define an open boundary.

Parameter File

We explain every part of this parameter file in detail. In each section of the parameter file, we describe relevant parameters. The omitted parameters are only user preference parameters and do not impact the simulation results. For more detail, we suggest visiting the Parameters Guide.

Simulation Control

subsection simulation control
  set method             = bdf2
  set bdf startup method = multiple step bdf
  set time step          = 0.0025 # Time step
  set time end           = 1.3    # End time of simulation
  set output name        = out    # Prefix for VTU outputs
  set output frequency   = 1      # Frequency of simulation output
end

• The method is set to bdf2 to have a second-order time-stepping method. This ensures a low error due to the time discretization in this case.

• The bdf startup method is set to multiple step bdf as we do not have an initial solution that allows us to generate previous time steps. We use a multiple step bdf approach that will ramp the order of the scheme in the first few time steps.

• The time step is set to 0.0025. This ensures a low error due to the time discretization for this case.

• The time end is set to 1.3. This is slightly longer than the experimental results of Ten Cate et al. [1]. This ensures that the entire trajectory of the particle has been simulated.

Physical Properties

subsection physical properties
  subsection fluid 0
    set kinematic viscosity = 0.6041666666666
    set density             = 0.000960
  end
end

• The kinematic viscosity is set to 0.6041666666666. This value is derived from the case description by dividing \(\mu_f\) by \(\rho_f\).

FEM

subsection FEM
  set velocity order = 1
  set pressure order = 1
end

Here we use Q1-Q1 elements. This case is only for demonstration purposes as such we want to propose a simulation that is not too costly to run.

Mesh

subsection mesh
  set type               = dealii
  set grid type          = subdivided_hyper_rectangle
  set grid arguments     = 5,8,5: 0,0,0 : 10 , 16 ,10 : true
  set initial refinement = 1
end

The domain is a rectangular box as such we can directly use a subdivided hyper rectangle mesh from the deal.II library. In this case, we have orientated the y-direction with gravity. As such, we have the long side of the box along this axis.

• The grid arguments is set to 5,8,5: 0,0,0 : 10 , 16 ,10 : true. This section has 3 subsections. First 5,8,5 describes the initial subdivision of the box. This subdivision has been chosen as it is the smallest mesh we can do of the box in order to have cubic elements. Secondly 0,0,0 : 10 , 16 ,10 describes the 2 points from which we have derived the rectangular box (0,0,0) and (10,16,10). Finally, we have true, which is a boolean to activate the coloration of the boundary. This allows us to define separate boundary conditions at each side of the box.

• The initial refinement is set to 1. This will ensure to have a base mesh that is a bit smaller than the particle.

Mesh Adaptation

subsection mesh adaptation
  # Fraction of coarsened elements
  set fraction coarsening = 0.3

  # Fraction of refined elements
  set fraction refinement = 0.05

  # How the fraction of refinement/coarsening are interepreted. Choices are
  # <number|fraction>.
  set fraction type = number

  # Frequency of the mesh refinement
  set frequency = 1

  # Maximum number of elements
  set max number elements = 750000

  # Maximum refinement level
  set max refinement level = 6
  # minimum refinement level
  set min refinement level = 0

  # Type of mesh adaptationChoices are <none|uniform|kelly>.
  set type = kelly

  # Variable for kelly estimationChoices are <velocity|pressure>.
  set variable = velocity
end

• The fraction coarsening is set to 0.3. This limits the accumulation of elements when the particle is moving. It allows for cells far from the particle to be coarsened when the particles get further away.

• The fraction refinement is set to 0.05. The objective here is to refine elements that become close to the particle when it’s moving. This will mostly refine elements around the particle that are not included in the refinement zone around the particle. The refinement zone around the particle will be discussed in more detail in the IB particle section.

• The set frequency is set to 1. Since the particle is moving at each time step, the refinement zone around it should be reevaluated at each time step.

• The max refinement level is set to 6. This parameter limits how small the elements around the particle can get limiting the total number of elements in the problem. Here we limit the mesh size to 48 elements per diameter of the particle. This should be sufficient to get accurate results.

• The type is set to kelly. Since the particle is moving and we do not want a uniform refinement of all the cells, we use the kelly error estimator based on the velocity variable.

Boundary Conditions

subsection boundary conditions
  set number = 6
  subsection bc 0
    set id   = 0
    set type = noslip
  end
  subsection bc 1
    set id   = 1
    set type = noslip
  end

  subsection bc 2
    set id   = 2
    set type = noslip
  end
  subsection bc 3
    set id   = 3
    set type = outlet
    set beta = 0
  end
  subsection bc 4
    set id   = 4
    set type = noslip
  end
  subsection bc 5
    set id   = 5
    set type = noslip
  end
end

Here we define the 5 no slip boundary for all the box walls and specify the boundary with id=3 to an outlet representing the top of the box. We refer the reader to the Boundary Conditions - CFD section on how those boundaries are defined.

Note

The boundary id of dealii rectangular mesh are numbered as such: \(x_{min}=0\), \(x_{max}=1\), \(y_{min}=2\), \(y_{max}=3\), \(z_{min}=4\), \(z_{max}=5\).

Initial Conditions

subsection initial conditions
  # Type of initial conditionChoices are <L2projection|viscous|nodal>.
  set type = nodal
  subsection uvwp
    set Function expression = 0; 0; 0;0
  end
end

The initial condition for this case is simple to define. At the start of the simulation, we assume that the particle and the fluid are at rest. From there, we define a uniform velocity field of 0 everywhere. To do that, we used the type = nodal and then specified a function expression of 0 for all the velocity components.

Non-linear Solver

subsection non-linear solver
  subsection fluid dynamics
    set verbosity             = verbose
    set tolerance             = 1e-6
    set max iterations        = 10
    set residual precision    = 5
    set force rhs calculation = true
  end
end

• The tolerance is set to 1e-6. This is small enough to ensure that the flow field is adequately resolved, as here, we expect a velocity of the particle of the order of 10.

• The max iterations is set to 10. The objective here is to allow enough Newton non-linear steps to ensure the convergence to the tolerance. Also, we should limit the time pass on a single time step if the system is too stiff.

• The force rhs calculation is set to true. This is the most important modification with most of the other examples. By default, the non-linear solver will recalculate the RHS only after the update of the solution. But here, we need to evaluate it before every matrix resolution, and we cannot use the last RHS evaluation that was done after the last newton iteration. The particle position was updated between these two steps, changing the RHS evaluation. This means that for every non-linear step, we evaluate the RHS twice. The non-linear solver follows this sequence of steps for each newton iteration.

  • update the particle position

  • update the Jacobian matrix

  • update the RHS

  • solve the matrix system

  • reevaluate the RHS to check the convergence.

Linear Solver

subsection linear solver
  subsection fluid dynamics
    set method                                = gmres
    set max iters                             = 1000
    set relative residual                     = 1e-4
    set minimum residual                      = 1e-11
    set preconditioner                        = ilu
    set ilu preconditioner fill               = 0
    set ilu preconditioner absolute tolerance = 1e-20
    set ilu preconditioner relative tolerance = 1.00
    set verbosity                             = verbose
    set max krylov vectors                    = 1000
  end
end

• The method is set to gmres. This solver is less computationally expensive than the other option, and this case does not require any special preconditioner. This makes the gmres solver with ilu preconditioner the best option available.

• The max iters is set to 1000. This is a lot more steps than how much it should take to solve the system.

• The max krylov vectors is set to the same number as the maximum solver iterations. This is to ensure that we keep the full Arnoldi basis for each new iteration. From experience keeping a maximum of Krylov vector results in a faster resolution for this case than clearing the basis after a certain number of gmres iterations.

• The relative residual is set to 1e-4. This is small enough, so we don’t under-resolve our matrix and do extra non-linear steps because of it, and at the same, it doesn’t require too many gmres iterations.

• The ilu preconditioner fill is set to 0. This is the cheapest option. In this case, we can use this option without having to do too many gmres iterations. It requires less computational time to do a few more gmres iterations than building the preconditioner and doing fewer gmres iterations.

IB Particles

subsection particles
  set assemble Navier-Stokes inside particles = false
  set number of particles                     = 1
  subsection extrapolation function
    set length ratio  = 2
    set stencil order = 3
  end

  subsection local mesh refinement
    set initial refinement                = 6
    set refine mesh inside radius factor  = 0.8
    set refine mesh outside radius factor = 1.3
  end

  subsection DEM
    set particle nonlinear tolerance = 1e-5
    subsection gravity
      set Function expression = 0;-981;0
    end
  end

  subsection particle info 0
    set type             = sphere
    set shape arguments  = 0.75
    set integrate motion = true
    subsection position
      set Function expression = 5;12.75;5
    end
    subsection velocity
      set Function expression = 0;0;0
    end

    subsection physical properties
      set density         = 0.001120
    end
  end
end

In this subsection, we define most of the parameters that are related to the particle.

• The number of particles is set to one as we only want one particle.

• stencil order is set to 3 as this is the highest order we can use for this case, and it will not lead to Runge instability.

• refine mesh inside radius factor is set to 0.8. This creates a mesh refinement around the particle that avoids having hanging nodes in the calculation and helps ensure a small enough mesh around the particle.

• refine mesh outside radius factor is set to 1.3. This creates a mesh refinement around the particle that avoids having hanging nodes in the calculation and helps ensure a small enough mesh around the particle.

• initial refinement is set to 6. Here we want to have the mesh as small as possible for the first time step. To achieve this, we refine every element with at least one vertex in the refinement zone around the particle 6 times before the simulation starts. This ensures that all the cells in the refinement zone around the particle is as small as possible. This number of refinements is 1 more than necessary. This is to avoid having part of the particle not properly refined as the initial mesh is big enough that some elements cut by the IB may not be properly detected at the beginning of the process. Doing one more refinement ensures that all the elements are properly refined.

• integrate motion is set to true because we are interested in the dynamic of the particle as it sediments in the rectangular box.

• assemble Navier-Stokes inside particles is set to false because we are not interested in the flow inside of the particle.

• length ratio has been set to 2. This is small enough, so it does not impact too much the conditioning of the matrix while avoiding interpolation of the immersed boundary stencil in multiple elements.

• particle nonlinear tolerance has been set to 1e-5. This is small enough to ensure that the particle dynamics are adequately resolved. We expect a velocity of the particle of the order of 10.

• gravity Function expression is set to 0;-981;0 according to the definition of the case. As we choose the long axis of the rectangular box along the Y, we define gravity in this direction.

The following parameters are defined in the particle subsection.

• position Function expression is set to 5;12.75;5. This is the initial position of the particle according to the description of the case.

• velocity Function expression is set to 0;0;0. This is the initial velocity of the particle since it starts at rest.

• radius is set to 0.75. This is according to the definition of the case where the particle has a diameter of 1.5 cm.

• density is set to 0.001120. This is according to the definition of the case.

Running the Simulation

Call lethe-fluid-sharp by invoking the following command:

mpirun -np 14 lethe-fluid-sharp sedimentation-1-particle.prm

to run the simulation using fourteen CPU cores. Feel free to use more CPU cores.

Warning

Make sure to compile Lethe in Release mode and run in parallel using mpirun. This simulation takes \(\sim \, 4\) hours on \(14\) processes.

Results

In this section, we will briefly show some results of this simulation.

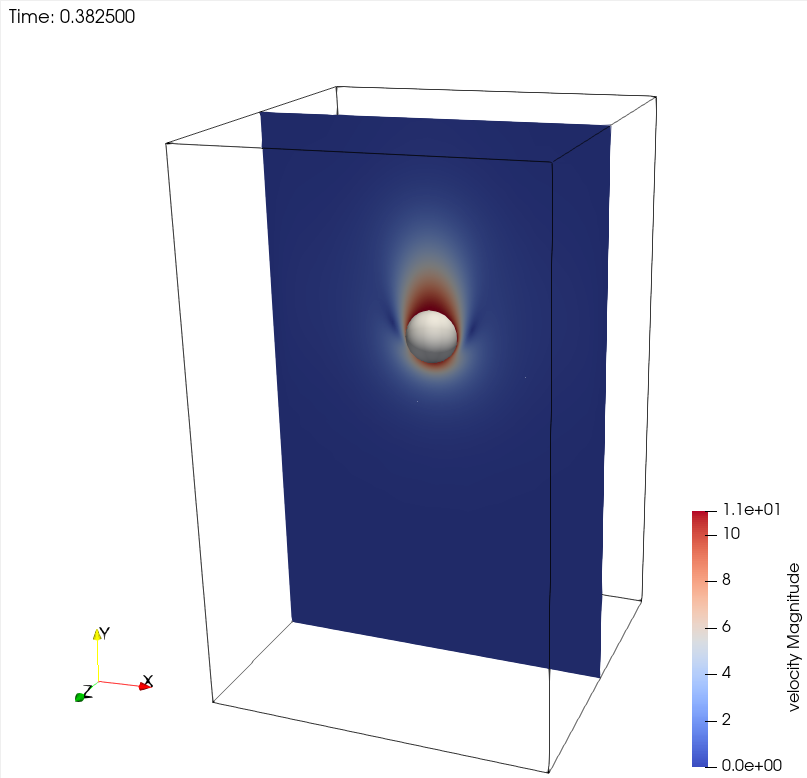
First, we look at a slice of the velocity profile during the acceleration phase.

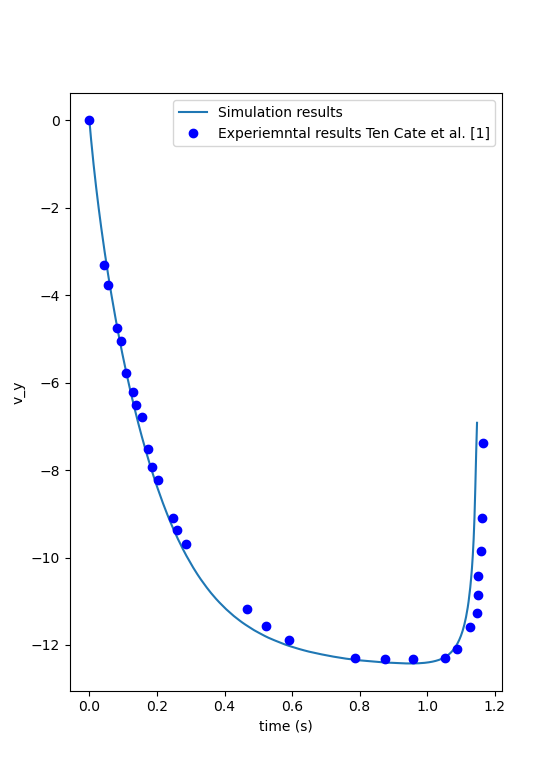
We can also compare the results obtained for the velocity in time with the results proposed by the article of Ten Cate et al. [1]

Reference

[1] (1,2,3)

A. ten Cate, C. H. Nieuwstad, J. J. Derksen, and H. E. A. Van den Akker, “Particle imaging velocimetry experiments and lattice-Boltzmann simulations on a single sphere settling under gravity,” Phys. Fluids, vol. 14, no. 11, pp. 4012–4025, Oct. 2002, doi: 10.1063/1.1512918.