Oblique Wall Impact#
This example of Lethe simulates the impact of a single aluminium oxide particle on a soda-lime glass wall using the Hertz collision model in 3D. This simulation is being setup according to MFIX DEM05 verification test [1] and comparisons are made with the experimental results of Kharaz, D.A. Gorham, and A.D. Salman [2]. It is recommended to visit DEM parameters for more detailed information on the concepts and physical meanings of the parameters in Lethe.
Features#
Solvers:
lethe-particlesPostprocessing using Python, PyVista, lethe_pyvista_tools
Files Used in this Example#
All files mentioned below are located in the example’s folder (examples/dem/3d-oblique-wall-impact).
Case generation Python script:
oblique_wall_impact_case_generator.pyParameter file for case generation:
oblique_wall_impact_template.tplPostprocessing Python script:
oblique_wall_impact_postprocessing.py
Description of the Case#
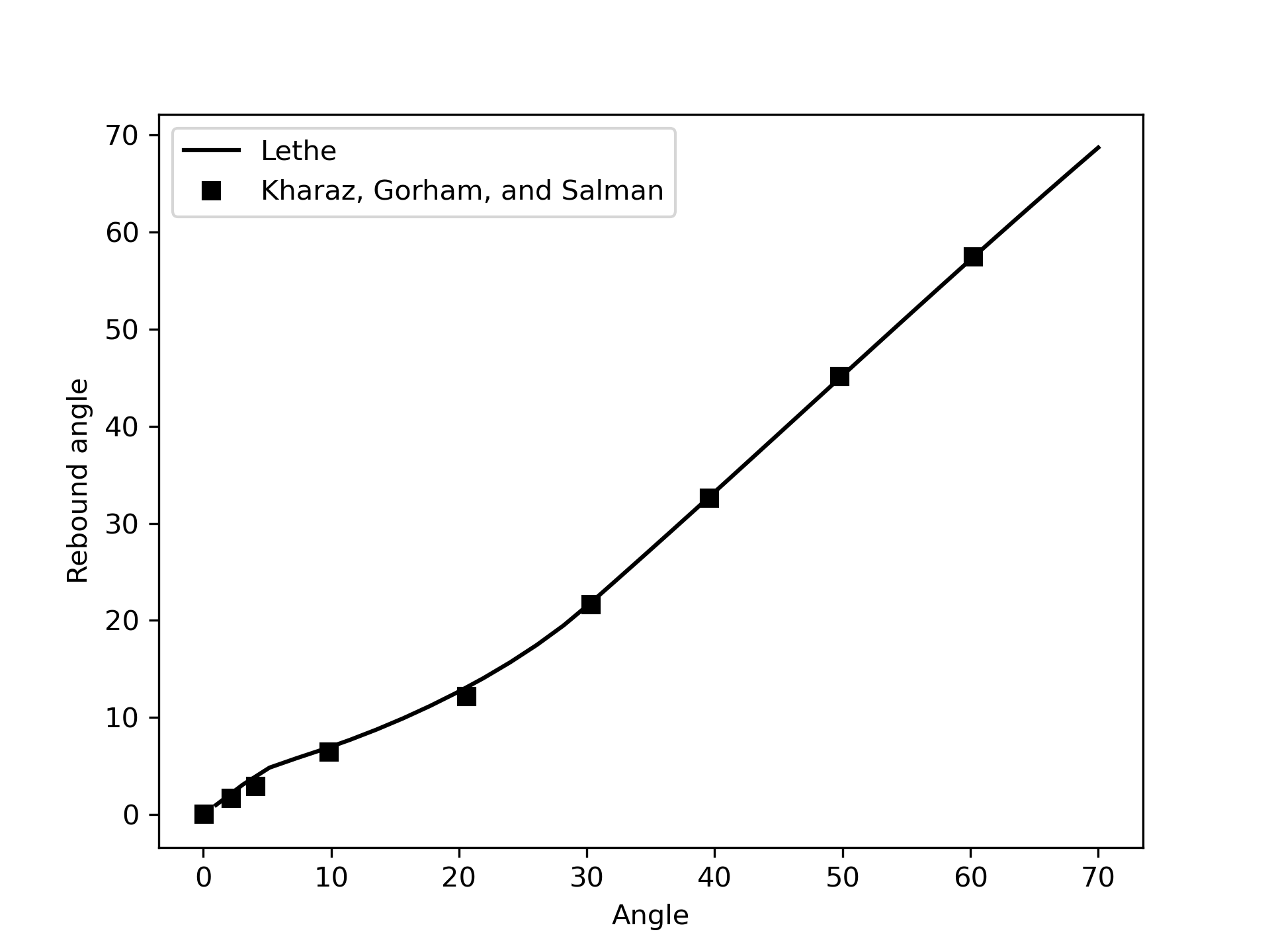
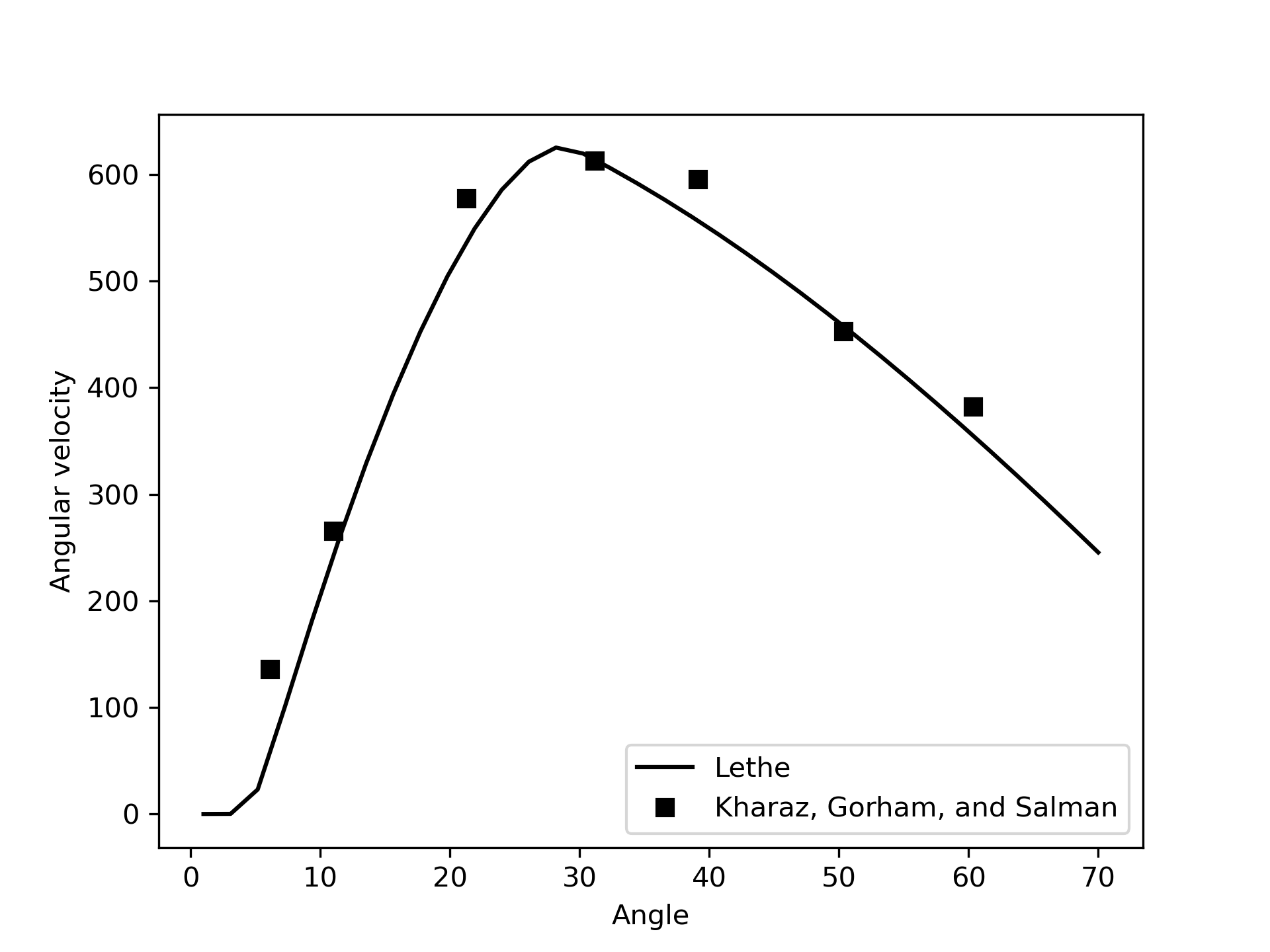
This simulation consists of a single particle bouncing at various angle on a flat plane in the absence of gravity. Depending on the angle of the contact, the particle will rebound at a different angle, angular velocity and tangential coefficient of restitution. In the present case, the tangential coefficient of restitution is defined as the ratio between the tangential velocity after rebound over the tangential velocity before rebound.
Parameter File#
Mesh#
The grid type in this example is not important. We use a hyper_cube. Its dimensions are 2.0 m in every direction (from 0.0 m to 2.0 m), and since only one particle is used, the refinement is set to zero.
subsection mesh
set type = dealii
set grid type = hyper_cube
set grid arguments = 0.0 : 2.0 : false
set initial refinement = 0
end
Insertion Info#
Since the insertion of the particle must be done at as specific height, the list insertion method is used. The insertion frequency can be set to any value, since we’re only using one particle. The particle is at a height of 0.005 m in the center of the X,Y plane. The velocity is not specified in the template file. It will be varied to set-up the angle, while keeping a magnitude of \(3.9\) m/s.
subsection insertion info
set insertion method = list
set insertion frequency = 10000
set list x = 1.
set list y = 1.
set list z = 0.005
set list velocity x = 0.0
set list velocity y = {{vy}}
set list velocity z = {{vz}}
set list omega x = 0.0
set list omega y = 0.0
set list omega z = 0.0
set list diameters = 0.005
end
Lagrangian Physical Properties#
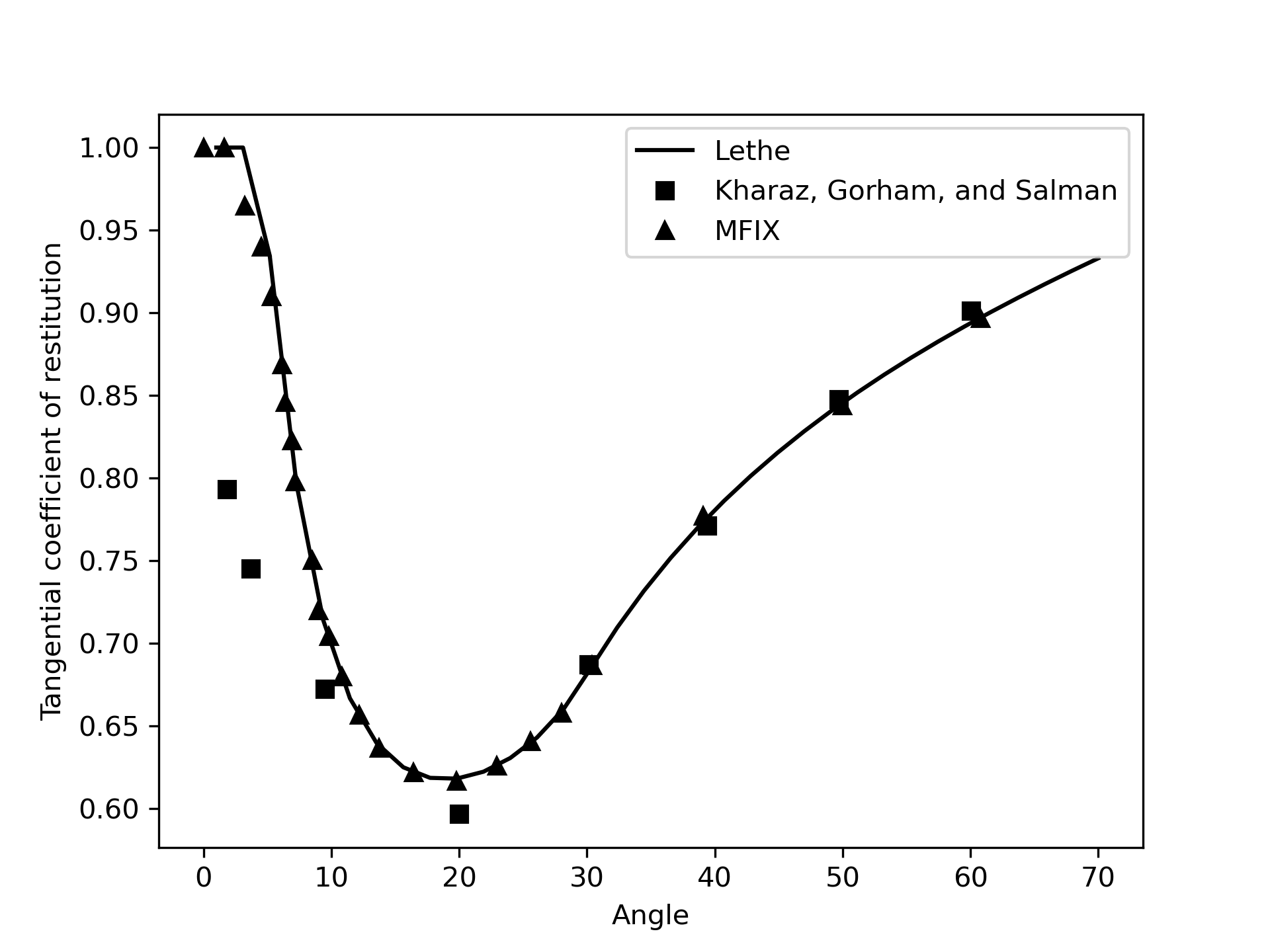
The particle is made of aluminium oxide and the wall is made of soda-lime glass. We use the physical properties of those material. Gravity is disabled. The sliding friction coefficient of the particles is set as the same used in the MFIX documentation.
subsection lagrangian physical properties
set g = 0.0, 0.0, 0.0
set number of particle types = 1
subsection particle type 0
set size distribution type = uniform
set diameter = 0.005
set number of particles = 1
set density particles = 4000
set young modulus particles = 380e9
set poisson ratio particles = 0.23
set restitution coefficient particles = 1.0
set friction coefficient particles = 0.092
end
set young modulus wall = 70e9
set poisson ratio wall = 0.25
set restitution coefficient wall = 1.0
set friction coefficient wall = 0.092
end
Model parameters#
We use a non-linear wall contact force model based on Hertz law. Rolling resistance is disabled since the particles considered in the experiments are perfectly spherical.
subsection model parameters
set particle particle contact force method = hertz_mindlin_limit_overlap
set particle wall contact force method = nonlinear
set integration method = velocity_verlet
set rolling resistance torque method = none
end
Generating the parameter files#
Using the following command:
Generates 34 file with the prefix run_oblique_impact_ and the {angle}.prm as a suffix.
Running the Simulation#
Once all files are created, the simulation can be launched in parallel using the following command:
Depending on the speed of your computer, all 34 simulation should be completed in less than two minutes. A folder named according to the angle of every simulation used will be generated (/xx).
Postprocessing#
A Python post-processing code called oblique_wall_impact_postprocessing.py is provided with this example. It is used to compare the rebound angle, the angular velocity and the tangential coefficient of restitution of the particles. Use the following line in your command line to run the post-processing code :
Important
You need to ensure that lethe_pyvista_tools is working on your machine. Click here for details.
A figure will be generated which compares the simulation results with the experimental data.
Results and Discussion#
Using the post-processing code, it is possible to compare the effect of the angle on the rebound angle, angular velocity and tangential coefficient of restitution.
First, we note the very good agreement between the rebound angle predicted and those obtained experimentally.
As for the angular velocity, there is a very good agreement between the results obtained with Lethe and the experimental results. It is interesting to note that the particle reaches a very high angular velocity (\(600\) rad/s).
The agreement for the tangential coefficient of restitution is less convincing, especially at low values of the impacting angle. The results obtained with the Hertz model of MFIX are superposed on this figure and they demonstrate that equivalent results are obtained with both MFIX and Lethe. Here, the disagreement between the results and the experiments is a consequence of the formulation of the Hertz model.