Sharp-Immersed-Boundary#
This subsection contains the parameters related to the sharp immersed boundary solver using a sharp interface immersed boundary (IB) method. This part of the parameter file concerns the usage of the lethe-fluid-sharp. This solver can simulate the flow around static or moving objects (with a predetermined trajectory). It can also simulate the coupled flow around spherical particles (Resolved CFD-DEM). Using this solver eliminates the need to define a conformal mesh for the fluid between the particles.
Note
All orientations and angular velocities in this solver use radians. The rotation sequence used to define the orientation of an object is the XYZ rotation.
subsection particles
set assemble Navier-Stokes inside particles = false
set number of particles = 1
subsection extrapolation function
set length ratio = 4
set stencil order = 2
set enable extrapolation = true
end
subsection output
set calculate force = true
set enable extra sharp interface vtu output field = false
set ib force output file = ib_force
set ib particles pvd file = ib_particles_data
set print DEM = true
end
subsection local mesh refinement
set initial refinement = 0
set refine mesh inside radius factor = 0.5
set refine mesh outside radius factor = 1.5
set refinement zone extrapolation = false
end
subsection DEM
set DEM coupling frequency = 1000
set alpha = 1
set contact search frequency = 1
set contact search radius factor = 3
set enable lubrication force = true
set lubrication range max = 2
set lubrication range min = 0.1
set particle nonlinear tolerance = 1e-6
set explicit contact impulsion = false
set explicit position integration = false
set approximate radius for contact = false
subsection gravity
set Function expression = 0; 0; 0
end
subsection wall physical properties
set wall friction coefficient = 0
set wall poisson ratio = 0.3
set wall restitution coefficient = 1
set wall rolling friction coefficient = 0
set wall youngs modulus = 100000000
end
end
subsection input file
set load particles from file = false
set particles file = particles
end
subsection particle info 0
set type = sphere
set shape arguments = 1
set integrate motion = false
set pressure location = 0; 0; 0
set mesh-based precalculations = true
set layer thickening = 0
subsection position
set Function expression = 0; 0; 0
end
subsection velocity
set Function expression = 0; 0; 0
end
subsection omega
set Function expression = 0; 0; 0
end
subsection orientation
set Function expression = 0; 0; 0
end
subsection physical properties
set density = 1
set volume = 0
set inertia = 1
set friction coefficient = 0
set poisson ratio = 0.3
set restitution coefficient = 1
set rolling friction coefficient = 0
set youngs modulus = 100000000
end
end
end
end
The
number of particlesis the number of particles simulated by the sharp-edge IB.The
assemble Navier-Stokes inside particlesparameter determines if the Navier-Stokes equations are solved inside the particles or not. If the Navier-Stokes equations are not solved (the parameter is false), the solver will solve a Poisson equation for each variable in the problem. This eliminates the need to define a reference value for the pressure.- The
extrapolation functionsubsection contains the parameters associated with the extrapolation function used to impose the sharp immersed boundary condition. The
stencil orderparameter controls the order of the Lagrange polynomial used to impose the sharp interface immersed boundary condition. The order of the stencil should be higher than or equal to the order of interpolation of the underlying FEM scheme (e.g. for Q2Q2 elements usestencil order=2). We suggest using the same order as the velocity field in most cases since it improves the condition number of the matrix.
Note
The stencil order used does not alter the order of convergence of the solution.
The
length ratioparameter controls the length of the zone used to define the Lagrange polynomial (see this article for more details). The length ratio should be kept as small as possible and above 1. When using a Cartesian homogenous mesh (aspect ratio of 1), the length ratio should be 1.
Tip
A good starting value is twice the average aspect ratio of the elements in the mesh multiplied by the order of the underlying FEM scheme.
The
enable extrapolationparameter controls if extrapolation is used to impose the immersed boundary condition. For debugging purposes, this parameter can be set tofalse; the particle velocity will then be imposed on velocity degrees of freedom of cells cut by the particle directly, which effectively amplifies the volume occupied by the solid.
Warning
Disabling the extrapolation is not recommended since it makes the Sharp-IB solver first-order accurate in space.
- The
- The
outputsubsection contains the parameters controlling the information printed in the terminal and output files. The
calculate forceparameter controls if the force is evaluated on each particle.The
ib force output fileparameter is the file name where the variables associated with each particle are stored. One file will be created for each particle in the simulation.The
ib particles pvd fileparameter is the file’s name that will be created to animate the particles. This file stores all the variables calculated for each of the particles. This file is compatible with Paraview.The
print DEMparameter is a boolean that define if particles’ informations are printed on the terminal when particles’ time-step is finished.When the
enable extra sharp interface vtu output fieldparameter is set totrue, it enables the output of additional value fields in the vtu file produced by the simulation. Currently, these additional output fields consist of: the id of the cell that cuts a specific cell (cell_cut).
- The
- The
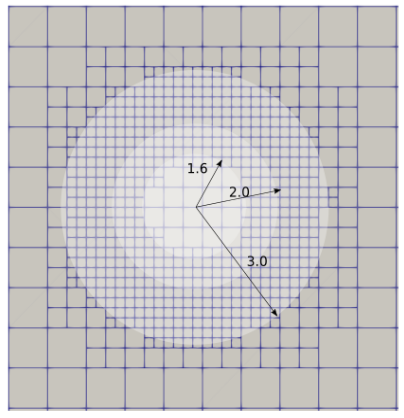
local mesh refinementsubsection contains the parameters associated with the local refinement around the particle. This refinement aims to form a near-surface zone of refined cells between two thresholds: \(\textit{inside factor} * \textit{radius}\) and \(\textit{outside factor} * \textit{radius}\). An effective radius, for non spheres, is calculated at the shape initialization and its definition is given further below. The
initial refinementparameter controls the number of refinement cycles in the near-particle refinement zone around every particle before the simulation starts.The
refine mesh inside radius factorparameter defines how deep inside the solid that cells can be refined. If the absolute distance between a cell’s degree of freedom and the solid’s surface is lower than \((1 - \textit{inside factor}) * \textit{radius}\), one of the two required conditions to refine this cell is met. For example: with a particle radius of 2 and the inside radius factor of 0.8, the inside reach of the refinement zone would be 0.4 (see example below).The
refine mesh outside radius factorparameter defines how far outside the solid that cells can be refined. If the absolute distance between a cell’s degree of freedom and the solid’s surface is lower than \((\textit{outside factor} - 1) * \textit{radius}\), the second of the two required conditions to refine this cell is met. For example: with a particle radius of 2 and the outside radius factor of 1.5, the outside reach of the refinement zone would be 1 (see example below).
Warning
The
mesh adaptation typemust bekellyto use the near-particle refinement around particles; otherwise, no near-particle refinement will happen. See Mesh Adaptation for more details on adaptative mesh refinement.Note
The refined cells are all those for which at least one of the degrees of freedom (dof) location satisfies both the
refine mesh inside radius factorand therefine mesh outside radius factorthresholds. Each cycle of refinement reduces the length of the elements by a factor two.Note
Using values
refine mesh outside radius factor = 1andrefine mesh inside radius factor = 1activates a minimal refinement mode. This enables the solver to select automatically the smallest region near the particle that guarantees stability of the solution.Note
This near-particle zone will be systematically refined at each refinement step until reaching the
max refinement levelparameter (Mesh Adaptation).The
refinement zone extrapolationparameter controls how the refinement zone is evaluated. By default, the refinement zone is around the particle’s last position (If this parameter is false). If this parameter is set to true, the refinement zone position is extrapolated from the particle’s current velocity. It will then apply all the initial refinement steps at the particle’s new position. This is used when the particle moves significantly between two time steps.
- The
- The
DEMsubsection contains all the parameters associated with the motion and contacts of spherical particles. The
DEM coupling frequencyparameter controls the number of iterations done on the DEM side for each CFD time step. It’s necessary to use a much smaller time step for the particle dynamics than for the fluid in case of contact between the particles. The particle collision happens at a much smaller time-scale than the fluid dynamics.The
alphaparameter is the relaxation parameter used when solving the dynamics equation of the particle.The
contact search frequencyparameter is used to set the updating frequency of the contact search list. By default, it is set to 1, which means that the contact search list is updated at each time-step.The
contact search radius factorparameter is used to create the list of potential contacting particles. Two given particles with respective radii \(R_1\) and \(R_2\) are in potential contact if the distance between them is < \((R_1 + R_2) * factor\). The default value of this parameter is set to 3.
Note
If all particles may be taken into account in the contact search, a large value of
contact search radius factorshould be set.Warning
If
contact search radius factor\(\leq 1\), an error is thrown.The
enable lubrication forceparameter enables or disables the use of lubrication forces. This parameter must be set tofalsewhen using a non-newtonian fluid rheology.
The
explicit contact impulsionparameter enables or disables the use of explicit contact impulsion evaluation in the resolution of the coupling of the particle. When it is set to true, this parameter results in the code only performing the DEM calculation once per CFD time step and using the resulting contact impulsion to evaluate all the other Newton’s iterations. This reduces the number of times the DEM calculation is made. However, since the position is still implicitly evaluated in the absence of contact, the cut cell mapping must be performed at each Newton iteration.The
explicit position integrationparameter enables or disables the use of explicit position integration in the resolution of the coupling of the particles. When it is set to true, this parameter results in the code only performing the DEM calculation once and using the resulting position and orientation to evaluate all the other Newton’s iterations. This reduces the number of times the cut cell mapping must be performed and the number of call to the DEM calculations. However, this can affect the stability of the scheme.The
approximate radius for contactparameter enables or disables the use of the approximate contact radius for contact calculation. When this parameter is true, the contact radius used in the contact force calculation is obtained through the effective contact radius. Otherwise, the curvature radius of the shape is evaluated at the contact point. In the case of a flat surface contact point, the contact radius is limited to 100 times the effective radius of the particle.
Note
When using a non-Newtonian fluid, the lubrication force will be automatically deactivated.
The
lubrication range maxparameter defines the distance below which the lubrication force between 2 particles or between a particle and a wall is calculated. The range is defined as a multiple of the smallest cell. The lubrication force model is used to model the force between particles when they are too close to each other to accurately resolve the flow between them.The
lubrication range minparameter defines the minimal distance used in the lubrication force calculation. The range is defined as a multiple of the smallest cell. This limits the force that can be applied on a particle since the lubrification force has a singularity when the distance between 2 particles is 0. We use this parameter to define a lower bound on the distance between 2 particles for the force calculation to avoid this singularity. Physically, this distance can be interpreted as the surface roughness of the particles.
Note
The lubrication force between two particles is expressed by the equation \(\mathbf{F_{lub_{ij}}} = \frac{3}{2} \pi \mu_f \left(\frac{d_{p_i} d_{p_j}}{d_{p_i}+d_{p_j}}\right)^2 \frac{1}{y}(\mathbf{v_{ij}}\cdot \mathbf{e_{ij}})\mathbf{e_{ij}}\). Where \(\mu_f\) is the fluid viscosity, \(d_{p_i}\) the diameter of the first particle, \(d_{p_j}\) the diameter of the second particle, \(y\) the gap between the two particles, \(\mathbf{v_{ij}}\) the relative velocity of the two particles, \(\mathbf{e_{ij}}\) the unit vector along the line that joint the centroide of the two particles. In the case of particle wall lubrication force we take the diameter of the second particle to be infinity [1]. This model requires a constant viscosity and density of the fluid.
The
particle nonlinear toleranceparameter controls particle dynamics’ nonlinear tolerance. The nonlinear solver won’t have converged until the residual on the dynamics equations of all the particles is smaller than this threshold.The subsection
gravitydefines the value of the gravity used in the simulation. This gravity can be defined as a function that evolves in time and space. Each component of theFunction expressioncorresponds respectively to its magnitude in X, Y, and Z.- The
wall physical propertiessubsection contains the properties of the wall that are used if the particle impact one of the boundaries of the domain. The effective properties used for calculating the impact force are calculated using a harmonic mean of the properties of the wall and the particle. The
wall friction coefficientparameter is the coefficient of friction of the wall. This parameter is used to define the effective coefficient of friction between the wall and the particles.The
wall poisson ratioparameter is the Poisson’s ratio of the wall’s material. This parameter is used to define the nonlinear spring constant used when a particle impacts a wall.The
wall restitution coefficientparameter is the restitution coefficient of the wall’s material. This parameter is used to define the effective restitution coefficient for the impact of a particle and the wall.The
wall rolling friction coefficientparameter is the rolling friction coefficient of the wall. This parameter is used to define the effective rolling friction coefficient between the wall and the particles.The
wall youngs modulusparameter is the Young’s modulus of the wall’s material. This parameter is used to define the nonlinear spring constant used when a particle impacts a wall.
Note
At this point in time, all the walls have the same properties.
- The
- The
- The
input filecontains the parameter needed if the particles are loaded from a file. The
load particles from fileboolean defines whether the particles are generated from an external file instead of the prm file. If this parameter is activated, the number of particles is defined directly from the file, that is, the particle’s subsection and the number of particles are ignored.
Warning
Currently, this feature works only for shapes defined by less than three parameters.
- The
particles fileis the file from which the particles are defined. Each line corresponds to a particle and all the relevant variables. The file must contain the following information for each particle (the header must be defined accordingly): type; shape_argument; p_x; p_y; p_z; v_x; v_y; v_z; omega_x; omega_y; omega_z; orientation_x; orientation_y; orientation_z; volume; density; inertia; pressure_x; pressure_y; pressure_z; youngs_modulus; restitution_coefficient; friction_coefficient; poisson_ratio; rolling_friction_coefficient; integrate_motion. Each column is separated by a semicolon (“;”). When a shape has multiple shape arguments, each argument is separated by a colon (“:”). If “integrate motion” is set to false, then the particle dynamic is not integrated. Otherwise, it is integrated. Here is a quick example of a particle definition. type; shape_argument; p_x; p_y; p_z; v_x; v_y; v_z; omega_x; omega_y; omega_z; orientation_x; orientation_y; orientation_z; volume ;density; inertia; pressure_x; pressure_y; pressure_z; youngs_modulus; restitution_coefficient; friction_coefficient; poisson_ratio; rolling_friction_coefficient; integrate_motion; superquadric; 1: 1: 1: 3: 3: 3; 0.25; 0.25; 20.25; 0.0; 0.0; 0.0; 0.0; 0.0; 0.0; 0.0; 0.0; 0.0; 0.001953125; 0.0015; 7.6698974609375e-08; 0.0; 0.0; 0.0; 1000000.0; 0.9; 0.0; 0.3; 0.0; true
- The
- The
The following parameter and subsection are all inside the subsection particle info 0 and have to be redefined for all particles separately.
The subsection
particle info 0is used to define relevant information that is specific to the particle with id0. For each particle with the indexn, a new subsection nameparticle info nshould be defined with relevant information.The
typeparameter is used to define the geometry type of the particle. The alternatives in 2D are:sphere,ellipsoid,hyper rectangle. In 3D, in addition to the previous shapes, alternatives include:cone,death star,cut hollow sphere,torus,cylinder,cylindrical tube,cylindrical helix,composite,rbf,opencascade. Anrbfgeometry is a flexible object described by a weighted sum of radial basis functions. The RBF data of an object can be generated from an STL file using a bitpit-based script, namely example RBF_example_00001.- The
shape argumentsparameter is used to define the parameters of the shape in the form of a list separated by;. The required arguments and the effective radius, used for near-particle refinement, are: Sphere: radius; the effective radius is the radius;
Hyper Rectangle: x half length, y half length, [z half length (if 3D)]; the effective radius is the Euclidian norm of the half lengths;
Ellipsoid: x radius, y radius, [z radius (if 3D)]; the effective radius is the Euclidian norm of the radii;
Torus: torus radius, torus thickness radius; the effective radius is the torus thickness radius;
Cone: tan(base angle), height; the effective radius is the height;
Cylinder: radius, half-length; the effective radius is the radius. The cylinder is aligned with the Z axis, and its center corresponds to the origin of its frame of reference.
Cylindrical Tube: hole radius, cylinder radius, half-length; the effective radius is the average between hole radius and cylinder radius. The tube is aligned with the Z axis, and its center corresponds to the origin of its frame of reference.
Cylindrical Helix: helix radius, extruded disk radius, helicoid height, pitch (height difference between each loop); the effective radius is the extruded disk radius.
Cut Hollow Sphere: radius, cut height, wall thickness; the effective radius is the radius;
Death Star: sphere radius, hole radius, distance between centers; the effective radius is the sphere radius;
Superquadric: x half length (or \(a\)), y half length (or \(b\)), z half length (or \(c\)), x exponent (or \(r\)), y exponent (or \(s\)), z exponent (or \(t\)); the effective radius is the Euclidian norm of the half lengths. The exponents represent the blockiness in each direction. The surface is implicitly described by \(\left|\frac{x}{a}\right|^r + \left|\frac{y}{b}\right|^s + \left|\frac{z}{c}\right|^t - 1 = 0\);
Composite: file name.
A composite shape is made from the composition, with boolean operations, of multiple primitive shapes (e.g., Sphere, Hyper Rectangle, Ellipsoid, Torus, Cone, Cylinder, etc). The composite shape has its own frame of reference that is used to place different primitives relative to each other. The position and orientation of the primitive objects are defined following the translation and then rotation in XYZ convention. The position and orientation of this object then define the position and orientation of the composite frame of reference in the global frame of reference. Note that the default position and orientation of a shape in a composite reference frame follow the same rule as it usually does in the global reference frame (for example, the cylinder is by default aligned in the Z-axis, and its center corresponds to the 0 of the reference frame). Composite shapes are defined by a text file that contains two sections that begin with their names:
shapesandoperations. All instructions are given on the lines following the section title in a similar syntax as the one from GMSH. For shapes, the syntax is:<shape_id>;<args separated by :>;<position components separated by :>;<orientation components separated by :>.For operations, the syntax is:<resulting_shape_id>;<union|difference|intersection>;<first shape id>:<second shape id>. In the case of difference, the first shape is the negative and the second shape is the positive. At this point in time, only these boolean operations have been implemented. Here is a general organization of a composite shape file.shapes <shape_id>; <shape type>; <shape arguments separated by:>; <position components separated by :> ; <orientation components separated by :> operations <resulting_shape_id>; <operation: union|difference|intersection>; <first shape id> : <second shape id>
Here is the content of a file that defines a cylinder topped with a sphere:
shapes 0; sphere; 0.5; 0:0:0.5 ; 0:0:0 1; cylinder; 0.5:0.5; 0:0:0.0 ; 0:0:0 operations 2; union; 0:1
Warning
Some limitations exist for composite shapes. The composition of shapes with union and difference are not always exact (see [this link](https://iquilezles.org/articles/interiordistance/) for a relatively simple explanation of why this is the case). In general boolean operations only guarantee to preserve the surface of the object. The union operation also preserves the properties of the signed distance function outside of the shapes, which is helpful for external flow around the shapes. But the difference operator does not guarantee to yield an exact signed distance function. This means that shapes defined by using the difference operator may not converge to the expected convergence order of the FEM scheme with the currently implemented scheme.
RBF: file name; the effective radius is the
support_radiusof the first node. The file must be constructed with 6 columns of numbers containing:weight,support_radius,basis_function,node_x,node_y,node_z. Theweightis the weight associated to each node, thesupport_radiusrelates to the influence radius of each node, thebasis_functioncan be one of thirteen functions, described in an upcoming example, and thenode_*describe the center of each node.OpenCascade: file name; the effective radius is the dim-root of the sphere that has the same volume as the shape. The OpenCascade shape allows the user to read .step file, .iges file, .stl file. From these files, a sign distance function is calculated. The .step file and the .stl file have a sign distance function. The .iges file has only a positive sign function assigned to them. Shapes defined by these files can significantly slow the simulation when they are in motion since the evaluation of the distance function of these shapes can be computationally intensive.
Note
As could be expected, using this type of shape requires that
dealiibe compiled with OpenCascade. This module can be installed with candi, by uncommenting the appropriate line incandi.cfg.
- The
The
integrate motionparameter controls if the dynamics equations of the particles are calculated. If this parameter is set to false, the particles’ position, velocity, and angular velocity are defined directly by the functions. Ifintegrate motion=truethe position and the velocity will be defined by the integration of the particle dynamic.Warning
Even though non-spherical particles can now have their dynamic coupled with the fluid, this feature is not yet fully validated and remains experimental at this point. We note the following limitations:
Particles can only have one point of contact between each other and with each wall. (this means contact detection for concave shapes may be wrong since these shapes can have more than 1 point of contact)
Fluid entrapment between particles can happen more frequently for non-spherical shapes in 3D (fluid entrapment occurs when a portion of the fluid domain becomes completely isolated from the rest of the fluid domain due to the imposition of the immersed boundary by multiple particles. A simple example of a case that causes fluid entrapment would be three circles in contact in 2D. Fluid entrapment leads to a zone without reference pressure, which is not a well-posed problem). In this case, the linear solver may fail to converge for a given Newton iteration.
The
mesh-based precalculationsparameter controls if the mesh-based precalculations are applied. These precalculations are critical for good performance in medium to high detailed RBFs (and its composites), but can introduce deformations. These deformations appear when some RBF nodes are located outside of the background mesh.The
layer thickeningis used to artificially inflate (positive value) or deflate (negative value) a particle. It can be used, for example, to evaluate the impact of uniform coating on a particle.The
pressure locationparameter is used to define the X, Y, and Z coordinate offsets of the pressure reference point relative to the center of the particle. These parameters are used when theassemble Navier-Stokes inside particlesparameter is set totrueto define the pressure reference point.The subsection
positiondefines the initial value of the particle position if the parameterintegrate motion=true. Otherwise, it defines the particle’s position at all points in time. This position is expressed as a function that can evolve in time. Each component of theFunction expressioncorresponds to the value of coordinates X, Y, and Z.The subsection
velocitydefines the initial value of the particle velocity if the parameterintegrate motion=true. Otherwise, it defines the particle’s velocity at all points in time. This velocity is expressed as a function that can evolve in time. Each component of theFunction expressioncorresponds to the value of its component in the X, Y, and Z directions.The subsection
orientationdefines the initial value of the particle’s angular position around each of the axes: X, then Y, and lastly Z.
Warning
The way position and orientation are defined is that the position of the solid is taken into account first, and then the orientation is considered. The orientation is considered as a rotation around each main axis, in the order X, then Y, and lastly Z. The center of rotation for this rotation is the position point of the solid.
Warning
Concerning omega and orientation, it’s important to note that even the 2D solver uses the rotational velocity in 3D. In that case, it will only use the Z component of the rotational velocity, but all three should be defined.
- The
physical propertiessubsection contains all the parameters associated with the particle physical properties. The
densityparameter is used to define the density of the particle.The
volumeparameter is used to define the volume of the particle. If the value is left to 0, then the volume is automatically calculated based on the shape. If the shape does not have a direct definition of its volume (for example, in the case of a superquadric shape), the volume is defined by the volume of a sphere with a radius equivalent to the effective radius of the shape.The
inertiaparameter is used to define one of the diagonal elements of the rotational inertia matrix. This parameter expects either a single value or a three-by-three matrix for the moments of inertia of the particle in the reference frame of the particle. The entry sequence corresponds to : I_xx ;I_xy ;I_xz ;I_yx ;I_yy ;I_yz ;I_zx ;I_zy ;I_zz. If a single value is given, the inertia is assumed to be uniform for all the axes.Tip
The current implementation does not support inertia matrices that are not diagonal and shapes where the center of mass does not fall on the origin of the particle’s reference frame. To avoid such a problem, we recommend using the composite shape to align and center the principal axis of the inertia matrix and the center of mass with the origin of the particle.
The following properties are used if the particle collides with one of the boundaries of the domain or another particle. The effective properties used to calculate the impact force are the harmonic mean between the properties of the colliding entities.
The
friction coefficientparameter is the coefficient of friction of the particle. This parameter is used to define the effective coefficient of friction between the wall and the particles.The
poisson ratioparameter is the Poisson’s ratio of the particle’s material. This parameter is used to define the nonlinear spring constant used when a particle impacts a wall.The
restitution coefficientparameter is the restitution coefficient of the particles’ material. This parameter is used to define the effective restitution coefficient for the impact of a particle and the wall.The
rolling friction coefficientparameter is the rolling friction coefficient of the particle. This parameter is used to define the effective rolling friction coefficient between the wall and the particles. The effective coefficient is calculated using a harmonic mean of the properties of the particles and the other objects it impacts.The
youngs modulusparameter is the Young’s modulus of the particle’s material. This parameter is used to define the nonlinear spring constant used when a particle impacts a wall.
- The
Tip
For a particle to be accounted for in the fluid mesh, it has to overlap at least one vertex of this fluid mesh. If the initial mesh is too coarse in regards to the particle size, the particle may not be captured if it does not intersect the outer mesh walls. To avoid this, a box refinement can be added around the particle (See Box refinement documentation).
Mesh refinement
The mesh is refined on multiple occasions during the simulations, and it can be slightly confusing to understand the sequence of refinement. There are 3 pre-simulation refinement steps. The first is the global mesh refinement. It is set by the initial refinement parameter in the mesh subsection.
The second refinement is inside the box refinement zone, set by the initial refinement in the box refinement subsection. Lastly, the near-particle zone is refined, defined by the initial refinement parameter in the particles subsection.
Therefore, the near-particle zone around each particle is refined mesh:initial refinement + box:initial refinement + particle:initial refinement times before the simulations starts.
Note
If the max refinement level parameter in the adaptation control subsection is smaller than the summation of all initial refinement parameters, no cell can be refined more than max refinement level. Note that it does not mean that the refinement stops, meaning that there can be other cells that are refined to the max refinement level, but no cell can be refined more than this.