Static Irradiation of a Bare Plate#

This example simulates the static irradiation of a Ti6Al4V bare plate. It is based on the experimental work of Cunningham et al. [1] and includes the relevant phenomena involved in the laser powder bed fusion manufacturing process.

Features#

Solver: lethe-fluid
Volume of fluid (VOF) and Heat Transfer (HT)
Unsteady problem with phase change handled by an adaptive BDF1 time-stepping scheme

Files Used in this Example#

All files mentioned below are located in the example’s folder (examples/multiphysics/static-irradiation).

Parameter file: 2D/static-irradiation.prm
Mesh file: mesh/bare-plate-2D.msh

Description of the Case#

Laser powder bed fusion is a manufacturing process using a laser to selectively melt and consolidate, layer-by-layer, a metal powder. Simply, it corresponds to 3D printing with a metal powder. The main laser-material interaction takes place at the melt pool scale where the flow dynamics involve multiple driving forces:

phase changes due to laser heating
surface tension effects due to the small scale of the melt pool
evaporative cooling and recoil pressure as temperature reaches the boiling point

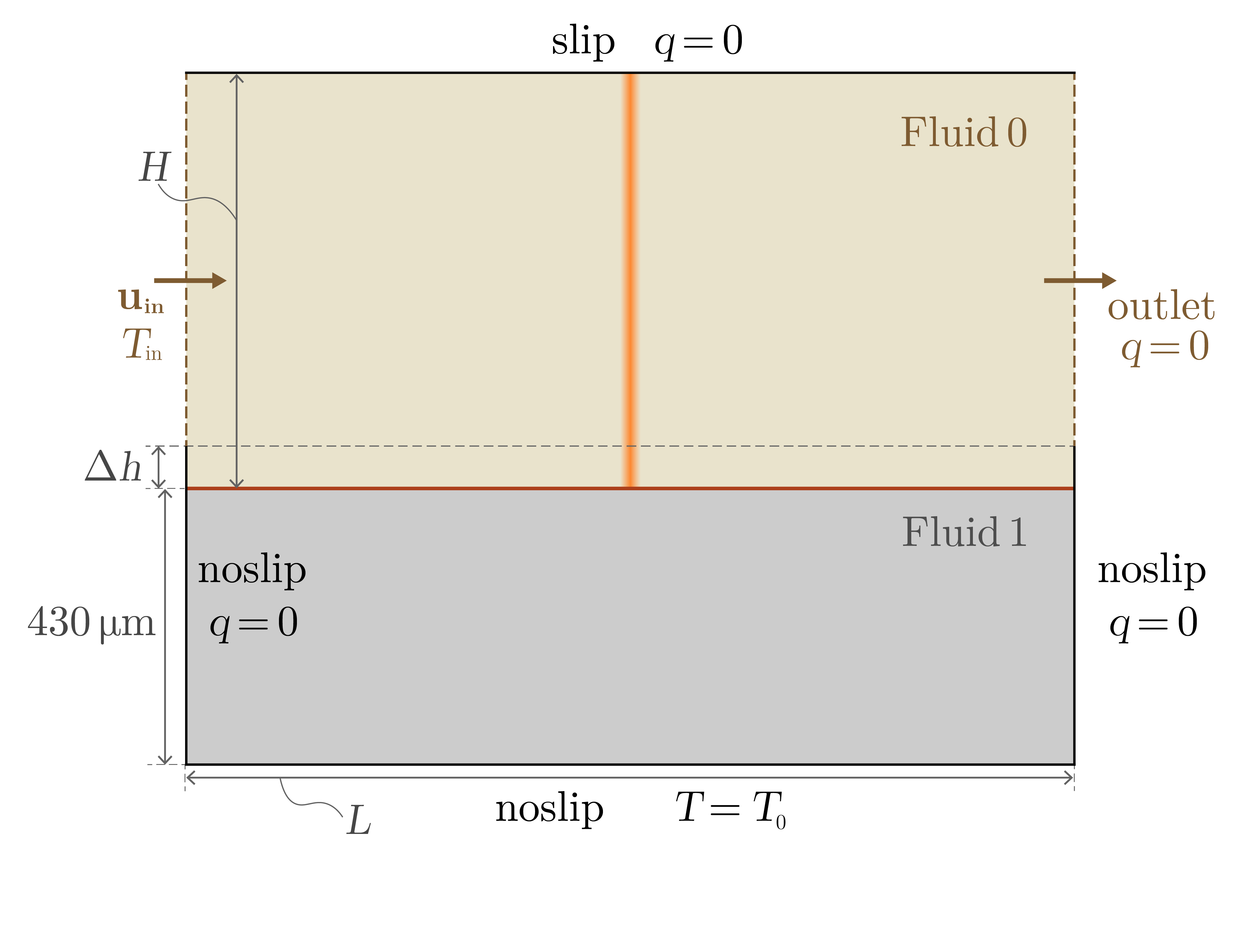
In this example, we consider the static irradiation of Ti6Al4V bare plate (without powder) in a building chamber backfilled with Argon to study the melt pool dynamics. We simulate an irradiation of \(0.5 \;\text{ms}\) by a laser beam with a diameter of \(140\;\mu\text{m}\) and a power of \(156\;\text{W}\). The following figure shows the case setup, which is based on the experimental work of Cunningham et al. [1]

The dimensions (\(H, \Delta h\), and \(L\)) and the Dirichlet boundary condition values (\(u_{\text{in}}, T_\text{in}\), and \(T_\text{0}\)) are listed bellow.

Parameter	Value	Parameter	Value
\(H\)	\(170\;\mu\text{m}\)	\(u_{\text{in}}\)	\(0.1\;\text{m s}^{-1}\)
\(\Delta h\)	\(20\;\mu\text{m}\)	\(T_{\text{in}}\)	\(298\;\text{K}\)
\(L\)	\(600\;\mu\text{m}\)	\(T_{\text{0}}\)	\(298\;\text{K}\)

There are three phases involved in this simulation: solid and liquid Ti6Al4V, and Argon. The metal-gas interface is handled by the VOF solver, while the solid-liquid interface is obtained from the temperature field of the HT solver. Hence, this example models a two-fluid problem: fluid 0 corresponds to the Argon phase and fluid 1 is the metal (solid and liquid), for which the solid part corresponds to a infinitely viscous fluid.

Note

To improve the performance of the solvers, all dimensional quantities in this example are based on the SI system except for the reference length, which is taken as \(1\;\text{mm}\). This scaling helps the matrices to have better conditioning, as explained for the pressure scaling in the stabilization subsection.

Parameter File#

Simulation Control#

The time integration is handled by a first order backward differentiation scheme (bdf1) with a maximum time-step of \(\Delta t = 1.9 \times 10^{-8} \; \text{s} < \Delta t_\sigma\) which corresponds to the capillary time-step constraint (see capillary wave example). We use adaptive time stepping with a maximum CFL of \(0.06\) to prevent instability resulting from the explicit coupling between the NS and HT solvers through the recoil pressure and evaporative cooling.

subsection simulation control
  set method           = bdf1
  set time end         = 0.0005
  set time step        = 1.9e-8
  set adapt            = true
  set max cfl          = 0.06
  set max time step    = 1.9e-8
  set output name      = static-irradiation
  set output path      = output/
  set output frequency = 100
end

Multiphysics#

In the multiphysics subsection, we enable both the VOF and HT solvers.

subsection multiphysics
  set VOF           = true
  set heat transfer = true
end

Mesh Adaptation#

As the laser heats the metal-gas interface, a vapor depression forms and deepens, and the liquid-gas interface reaches the bottom boundary of the box refinement. Hence, we dynamically adapt the mesh using the temperature as the refinement variable to keep a well discretized interface. We choose \(7\) as the min refinement level and \(4\) as the max refinement level. The mesh is adapted each \(20\) iterations to reduce the computational cost by setting frequency = 20. Note that the fraction coarsening is set to \(0.0\) to avoid coarsening in the center of the melt pool, where the temperature gradient, used by the Kelly error estimator, is less important than at the liquid-gas interface.

subsection mesh adaptation
  set type                 = kelly
  set variable             = temperature
  set fraction type        = fraction
  set max refinement level = 7
  set min refinement level = 4
  set frequency            = 20
  set fraction refinement  = 0.4
  set fraction coarsening  = 0.0
end

Boundary Conditions#

In the boundary conditions subsection, we set the boundary conditions described in the figure above for the NS, HT, and VOF solvers. The following subsection boundary conditions sets the NS boundary conditions:

subsection boundary conditions
  set number = 6
  subsection bc 0
    set id   = 2 # bottom wall
    set type = noslip
  end
  subsection bc 1
    set id   = 5 # bottom part of the right wall
    set type = noslip
  end
  subsection bc 2
    set id   = 6
    set type = outlet # top part of the right wall
    set beta = 0
  end
  subsection bc 3
    set id   = 7
    set type = slip # top wall
  end
  subsection bc 4
    set id   = 4 # top part of the left wall
    set type = function
    subsection u
      set Function expression = 100.0
    end
    subsection v
      set Function expression = 0
    end
  end
  subsection bc 5
    set id   = 3 # bottom part of the left wall
    set type = noslip
  end
end

In subsection boundary conditions heat transfer, we set the boundary conditions for the HT solver:

subsection boundary conditions heat transfer
  set number = 6
  subsection bc 0
    set id   = 2  # bottom wall
    set type = temperature
    subsection value
      set Function expression = 298
    end
  end
  subsection bc 1
    set id   = 5 # bottom part of the right wall
    set type = noflux
  end
  subsection bc 2
    set id   = 6 # top part of the right wall
    set type = noflux
  end
  subsection bc 3
    set id   = 7 # top wall
    set type = noflux
  end
  subsection bc 4
    set id   = 4 # top part of the left wall
    set type = temperature
    subsection value
      set Function expression = 298
    end
  end
  subsection bc 5
    set id   = 3 # bottom part of the left wall
    set type = noflux
  end
end

Note

We recover the id of each boundary at the end of the mesh file generated with Pointwise (mesh/bare-plate-2D.msh):

$PhysicalNames
6
1 2 "bottom"
1 3 "left_bottom"
1 4 "left_top"
1 5 "right_bottom"
1 6 "right_top"
1 7 "top"
$EndPhysicalNames

Here, the id corresponds to the second column and we identify the corresponding boundary in the domain with the description given in the third column.

For the sake of brevity, we leave out the subsection boundary conditions VOF because they all corresponds to no flux boundary conditions (none). However, in the example’s parameter file, all boundary conditions are defined.

Initial Conditions#

In the initial conditions subsection, we set the initial condition for all the solvers:

NS intial conditions are \(0.0\) for both velocity components and for the pressure
HT intial condition corresponds to a uniform temperature \(T_\text{0} = 298\;\text{K}\)
VOF intial condition allows us to described the metal and gas phases. The bottom part of the domain (\(y<430\;\mu\text{m}\)) corresponds to the Ti6Al4V metal phase (fluid 1), while Argon (fluid 0) fills the top part.

subsection initial conditions
  set type = nodal
  subsection uvwp
    set Function expression = 0; 0; 0
  end
  subsection temperature
    set Function expression = 298
  end
  subsection VOF
    set Function expression = if (y<0.43 , 1, 0)
  end
end

Physical Properties#

The physical properties subsection sets the material properties for the metal and gas phase. It is in this subsection that we activate the phase change by setting the solid and liquid properties for the metal phase, in the same fashion as in the Stefan problem and melting cavity examples. However, since we consider an alloy (TI6Al4V), the phase change occurs over a temperature range. Hence, the difference between the liquidus temperature and solidus temperature corresponds to the real temperature range in which the solid and liquid TI6Al4V coexist (mushy zone).

We also set in this subsection the reference surface tension coefficient of the metal-gas interface and its temperature derivative to simulate the Maragoni effect. Here, we consider a linear evolution of the surface tension coefficient with the temperature at the liquid-gas interface, and we neglect its effect at the solid-gas interface to avoid numerical instabilities. This is done by setting surface tension model = phase change. We refer to the parameter guide Physical Properties for more details on this model.

subsection physical properties
  set number of fluids = 2
  subsection fluid 1
    set density              = 4.42e-6
    set thermal conductivity = 2.88e4

    set thermal expansion model = phase_change
    set rheological model       = phase_change
    set specific heat model     = phase_change

    subsection phase change
      set liquidus temperature = 1928.0
      set solidus temperature  = 1878.0

      set viscosity liquid = 0.905
      set viscosity solid  = 9.05e4

      set specific heat liquid = 1.126e9
      set specific heat solid  = 0.8e9
      set latent enthalpy      = 2.9e11
    end
  end

  subsection fluid 0
    set density              = 1.784e-9
    set thermal conductivity = 18
    set kinematic viscosity  = 56.1
    set specific heat        = 5.20e8
  end

  set number of material interactions = 1
  subsection material interaction 0
    set type = fluid-fluid
    subsection fluid-fluid interaction
      set first fluid id                              = 0
      set second fluid id                             = 1
      set surface tension model                       = phase change
      set surface tension coefficient                 = 1.52
      set reference state temperature                 = 1928.0
      set temperature-driven surface tension gradient = -5.5e-4
      set liquidus temperature                        = 1928.0
      set solidus temperature                         = 1878.0
    end
  end
end

Laser parameters#

We defined the laser heat source in the laser parameters subsection. In the present example, we are considering the irradiation of a bare plate. Thus, the laser only heats the metal-gas interface and we model this surface heat flux using the gaussian_heat_flux_vof_interface laser model. We refer to the parameter guide Laser Heat Source for more details on this model.

subsection laser parameters
  set enable           = true
  set type             = gaussian_heat_flux_vof_interface
  set power            = 156e6
  set absorptivity     = 0.35
  set beam radius      = 0.07
  set start time       = 0
  set end time         = 0.002
  set beam orientation = y-
  subsection path
    set Function expression = 0.3; 0.43
  end
end

The laser is static in the middle of the domain at the metal-gas interface \(\vec{x} = [0.3, 0.43]\), hence its path is independent of the time. Note that the \(y\) component of the path is not relevant: the gaussian_heat_flux_vof_interface model applies the laser heat flux at the metal-gas interface no matter its postion along the \(y\) axis. This allows us to model the effect of the interface deformation on the surface heat flux.

Evaporation#

The cooling and the recoil pressure due to a fast, out of equilibrium, evaporation are driving forces in the energy and momentum balances, respectively. We active both terms in the evaporation subsection.

subsection evaporation
  set evaporation mass flux model = temperature_dependent
  set enable evaporative cooling  = true
  set enable recoil pressure      = true

  set evaporation coefficient     = 0.82
  set recoil pressure coefficient = 0.56
  set evaporation latent heat     = 8.9e12
  set molar mass                  = 4.58e-2
  set universal gas constant      = 8.314e6
  set boiling temperature         = 3550.0
  set ambient pressure            = 101.325
end

In this example, we consider the model of Anisimov and Khokhlov [2] to compute the evaporative cooling \(q_\text{evap}\) and the recoil pressure \(p_\text{rec}\):

\[q_\text{evap} = \phi_\text{evap} L_\text{vap} p_\text{sat}\sqrt{\frac{M}{2\pi R}}\]

\[p_\text{rec} = \psi_\text{evap} p_\text{sat}\]

where \(\phi_\text{evap}=0.82\) and \(\psi_\text{evap}=0.56\) are the evaporation coefficient and recoil pressure coefficient, respectively, \(L_\text{vap}=8.9\times 10^{6}\;\text{Jkg}^{-1}\) is the evaporation latent heat, \(M=4.58\times 10^{-2}\) is the molar mass of the metal, \(R=8.314\;\text{Jmol K}^{-1}\) is the universal gas constant and \(p_\text{sat}\) is the saturation pressure. The latter is computed according to:

\[p_\text{sat} = p_\text{atm}\exp{\left[\frac{L_\text{vap}M}{RT_\text{boil}}\left(1-\frac{T_\text{boil}}{T}\right)\right]}\]

where \(p_\text{atm}=101.325\;\text{kPa}\) is the ambient pressure, and \(T_\text{boil}=3550\;\text{K}\) is the boiling temperature.

Both terms are then applied at the liquid-gas interface using the Continuous Surface Force (CSF) model, as described for the surface tension in The Volume of Fluid (VOF) Method theory guide.

Non-Linear Solver#

The parameters for the non-linear system resolution of the three physiscs are set in the non-linear solver subsection.

subsection non-linear solver
  subsection fluid dynamics
    set tolerance      = 1e-4
    set max iterations = 20
    set verbosity      = verbose
  end
  subsection heat transfer
    set tolerance      = 100
    set max iterations = 20
    set verbosity      = verbose
  end
  subsection VOF
    set tolerance      = 1e-4
    set max iterations = 20
    set verbosity      = verbose
  end
end

We select the tolerances of the NS and HT non-linear solvers so that the norm of the velocity, pressure and temperature corrections make sense with the order of magnitude of the corresponding solution. For example, we set the tolerance on the residual of the HT solver to 100, resulting in a maximal correction of \(\text{O}(1\times 10^{-3})\) on the temperature, which is \(\text{O}(1\times 10^{3})\):

--------------
Heat Transfer
--------------
Newton iteration: 0  - Residual:  1.985e+07
  -Tolerance of iterative solver is : 1.985e+05
  -Iterative solver took : 2 steps to reach a residual norm of 3.944e+04
    alpha =      1 res = 1.583e+05  ||dT||_L2 =  71.89      ||dT||_Linfty = 15.46
Newton iteration: 1  - Residual:  1.583e+05
  -Tolerance of iterative solver is : 1583
  -Iterative solver took : 2 steps to reach a residual norm of 409.8
    alpha =      1 res =   1074     ||dT||_L2 = 0.3355      ||dT||_Linfty = 0.103
Newton iteration: 2  - Residual:  1074
  -Tolerance of iterative solver is : 10.74
  -Iterative solver took : 2 steps to reach a residual norm of 5.567
    alpha =      1 res =   5.47     ||dT||_L2 = 0.0111      ||dT||_Linfty = 0.001807

The linear solver tolerances are set accordingly.

Running the Simulation#

We call lethe-fluid to launch the simulation by invoking the following command from the 2D subdirectory:

mpirun -np 14 lethe-fluid static-irradiation.prm

Warning

Make sure to compile Lethe in Release mode and run in parallel using mpirun. This simulation takes \(\sim \, 24\) hours on \(12\) processes.

Results#

The following video shows on the left the temperature evolution in the metal, and on the right, the phase fraction evolution. We observe the melt pool, delimited by the black line, deepening and the formation of the vapor depression at the liquid-gas interface. This is often refered as a keyhole. It is caused by the recoil pressure, resulting from the fast out of equilibrium evaporation, and the Marangoni effect, driving melt alway from the melt pool center.

We also observe a air cushion forming at the triple-phase contact line. We assume it is linked to the fact that wetting is not modeled in the simulation. Thus, the implementation of a wetting model corresponds to a future addition in Lethe.