Jurin’s Law

This example simulates the capillary rise of a fluid between two planes caused by a constraint on the angle of contact between the wall and the fluid.

Features

• Solver: lethe-fluid (Q1-Q1)

• Two phase flow handled by the Cahn-Hilliard-Navier-Stokes (CHNS) approach

• Angle of contact boundary condition

• Dimensionality of the length

• Parametric sweep on the value of the angle of contact

• Post-processing of the height difference between the outside fluid and the meniscus

Files Used in This Example

All files mentioned below are located in the example’s folder (examples/multiphysics/jurins-law-2d).

• Pointwise mesh file: jurins-law-2d-dimensioned.pw

• Mesh file: jurins-law-2d-mesh-dimensioned.msh

• Parameter file: jurins-law-2d.prm

• Postprocessing Python script: jurins_law_multiple_folders.py (using the functions of postprocessing_jurins_law_dimensioned.py)

Description of the Case

Have you ever wondered why does your coffee goes up the sugar cube when it touches the surface of your drink? Or how the sap goes up in the tree? Or how the wax that keeps the flame of a candle alive is brought to the flame? These phenomena are all consequences of capillary action, a force that appears in narrow spaces and that seemingly opposes the gravitational forces. A simple case of capillary rise is described in this example, and compared to an analytical solution to check the implementation of our model. It consists of a 2D case, in which a dense fluid climbs the narrow space between two walls because of capillary actions.

Thanks to the symmetry of the problem, only one side is considered in the example. At \(t = 0\), a denser fluid (fluid 1) occupies the lower half of the domain with a lighter fluid (fluid 0) on the top. The wall is half-way submerged in both fluids. Because of the boundary condition imposing an angle of contact between the wall and the denser fluid, the surface is curved and a pressure gradient appears. Depending on the value of the angle, the height of the fluid will increase (or decrease) and reach an equilibrium height. The computational domain is described in the following figure (not to scale):

Representation of the initial (left) and final (right) states of the capillary rise

The quantity of interest of this problem is the difference in height (\(\Delta H\) in the figure above) between the tip of the meniscus and the surface of the fluid outside of the central part. The Jurin’s law [1] gives an asymptotic value of \(\Delta H\):

\[\Delta H = \frac{\sigma\cos{\alpha_c}}{\rho_1gR}\]

with \(\sigma\) the surface tension coefficient, \(\alpha_c\) the angle of contact imposed on the wall, \(\rho_1\) the density of the denser fluid, \(g\) the gravitational acceleration and \(R\) the half-distance between the walls.

Parameter File

Simulation Control

Time integration is handled by a 1st order backward differentiation scheme (bdf1), for a \(0.5 \ \text{s}\) simulation time with an initial time step of \(0.0005 \ \text{s}\). Time-step adaptation is enabled using adapt=true and the max CFL is \(0.8\). output boundaries is set to true to get a .vtu file containing the indices of the boundaries of the domain.

subsection simulation control
  set method            = bdf1
  set output name       = jurins-law-2d
  set output frequency  = 10
  set output path       = ./
  set max time step     = 5e-4
  set adapt             = true
  set max cfl           = 0.8
  set time end          = 0.5
  set time step         = 5e-4
  set output boundaries = true
end

Multiphysics

The multiphysics subsection is used to enable the cahn hilliard solver. Note that the fluid dynamics are solved by default.

subsection multiphysics
  set cahn hilliard = true
end

Dimensionality

The dimensionality subsection is used to define the unit length as \(0.001 \text{m} = 1 \ \text{mm}\). This setting helps with the convergence of the solver.

Note

When using the dimensionality parameters, the problem and the physical properties are rescaled using the new units specified by the user. This means that physical properties can be given their value in SI units and will automatically be rescaled. The resulting fields (velocity and pressure for instance) will also be rescaled accordingly. One exception to this is the source terms, which need to be specified in rescaled units.

subsection dimensionality
  set length = 0.001 # meter
end

Mesh

In the mesh subsection, we specify the mesh used in this example. The structured mesh used in this example was designed using Fidelity Pointwise. The source file is jurins-law-2d-dimensioned.pw. It was then exported into a readable format: jurins-law-2d-mesh-dimensioned.msh. The initial refinement is set to \(2\).

subsection mesh
    set type               = gmsh
    set file name          = ./jurins-law-2d-mesh-dimensioned.msh
    set initial refinement = 2
end

Mesh Adaptation

The mesh adaptation section controls the dynamic mesh adaptation. Here, we choose phase_cahn_hilliard as the refinement variable. The maximum and minimum refinement levels are respectively set to \(4\) and \(2\) with the number of initial refinement steps set to \(2\).

subsection mesh adaptation
  set type                     = kelly
  set variable                 = phase_cahn_hilliard
  set fraction type            = fraction
  set max refinement level     = 4
  set min refinement level     = 2
  set frequency                = 1
  set fraction refinement      = 0.99
  set fraction coarsening      = 0.1
  set initial refinement steps = 2
end

Physical Properties

The physical properties subsection defines the physical properties of the fluids. In this example, we need first to define the properties of the fluid rising due to the capillary effects. We set \(\rho_1 = 2000 \ \text{kg}\cdot\text{m}^{-3}\) and \(\nu_1 = 10^{-4} \ \text{m}^2\cdot\text{s}^{-1}\). The upper fluid should be much lighter, hence the choice of \(\rho_0 = 1 \ \text{kg}\cdot\text{m}^{-3}\). The surface tension coefficient was chosen equal to that of the water-air interface : \(\sigma = 0.073 \ \text{N}\cdot\text{m}^{-1}\).

Note

When using the Cahn-Hilliard solver, the mobility constant (\(D\)) is usually set proportionnal to \(\epsilon^2\), with \(\epsilon\) the interface thickness. This example does not follow this rule of thumb, and \(D\) had to be fine-tuned to get results coherent with the theory.

subsection physical properties
  set number of fluids = 2
  subsection fluid 0
    set kinematic viscosity        = 8e-5
    set density                    = 1
  end
    subsection fluid 1
    set kinematic viscosity        = 1e-4
    set density                    = 2000
  end
  set number of material interactions = 1
  subsection material interaction 0
    subsection fluid-fluid interaction
      set surface tension coefficient     = 7.3e-2
      set cahn hilliard mobility model    = constant
      set cahn hilliard mobility constant = 1e-7
    end
  end
end

Cahn-Hilliard

In the cahn hilliard subsection, we set the potential smoothing coefficient (soon to be deprecated) to \(0\). The interface thickness is set to be determined automatically based on the mesh size in the epsilon subsection. We also output the interface thickness for each time-step by setting the verbosity to verbose to know its exact value for the initial conditions.

subsection cahn hilliard
  set potential smoothing coefficient = 0

  subsection epsilon
    set method    = automatic
    set verbosity = verbose
  end
end

Initial Conditions

In the initial conditions subsection, we need only need to initialize the phase field in the cahn hilliard subsection. The chemical potential field is set to \(0\) uniformly. The interface is initialized with the equilibrium interface thickness, which requires to know the value of \(\epsilon\) that is outputted at every iteration. Here, \(\epsilon = 0.04419\).

subsection initial conditions
  subsection cahn hilliard
    set Function expression = tanh((y-4)/(sqrt(2)*0.04419));0
  end
end

Boundary Conditions

We need to set boundary conditions both for the fluid dynamics solver and the Cahn-Hilliard solver. For the latter, we constrain the angle of contact between the left side of the plate and the fluid using the angle_of_contact boundary condition of the Cahn-Hilliard solver.

subsection boundary conditions cahn hilliard
  set number = 4
  subsection bc 0
    set id          = 2
    set type        = angle_of_contact
    set angle value = 50
  end
  subsection bc 1
    set id   = 3
    set type = noflux
  end
  subsection bc 2
    set id   = 4
    set type = noflux
  end
  subsection bc 3
    set id   = 5
    set type = noflux
  end
end

Then, a slip boundary condition is applied everywhere, except for the upper boundary, where it is set as none.

subsection boundary conditions
  set number = 4
  subsection bc 0
    set id   = 2 # angle of contact
    set type = slip
  end
  subsection bc 1
    set id   = 5 # walls
    set type = slip
  end
  subsection bc 2
    set id   = 4 # upper surface
    set type = none
  end
  subsection bc 3
    set id   = 3 # middle
    set type = slip
  end
end

Source Term

In the source term subsection, we define the gravitational acceleration. Since the unit length is the millimeter, the usual value of \(g\) needs to be multiplied by \(1000\).

subsection source term
  subsection fluid dynamics
    set Function expression = 0; 0; -9810; 0
  end
end

Running the Simulation

We call lethe-fluid by invoking:

 mpirun -np 10 lethe-fluid jurins-law-2d.prm

to run the simulation using ten CPU cores. Feel free to use more CPU cores.

Warning

Make sure to compile Lethe in Release mode and run in parallel using mpirun. The simulation should take 3-4 minutes for 10 processors.

Results

The height difference is computed for different values of \(\alpha_c\) and compared to the Jurin’s law in the following figure, which shows an excellent agreement.

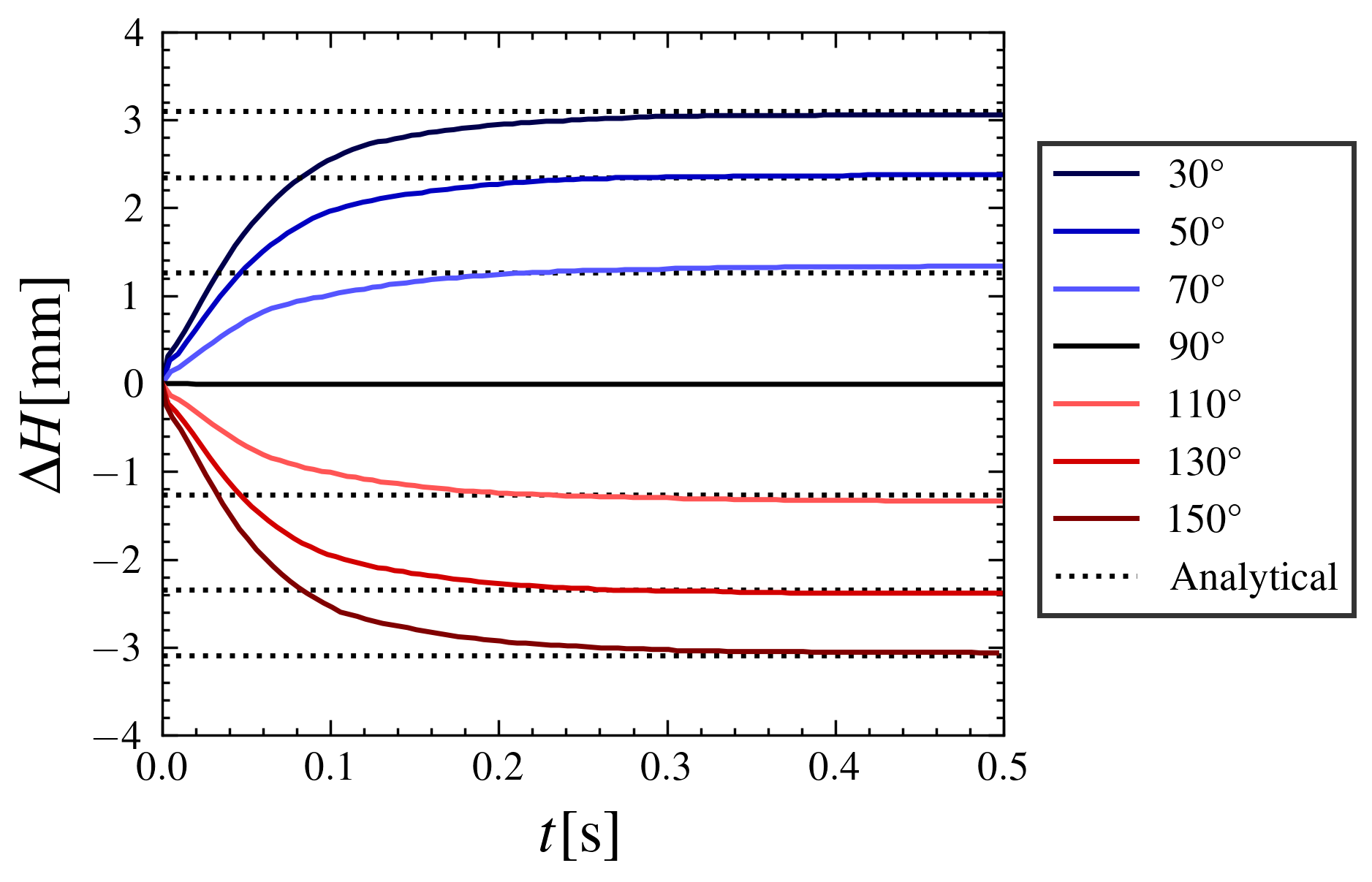
Height difference evolution for different angles of contact (>90° and <90°) with respect to time.

Furthermore, by visualizing the pressure fields in the vicinity of the meniscus at the end of the simulation, we observe in the following figure that they correspond well qualitatively to the pressure jumps predicted by Young-Laplace’s law. We conclude that the contact angle boundary condition is adequately coupled with the Navier-Stokes equations.

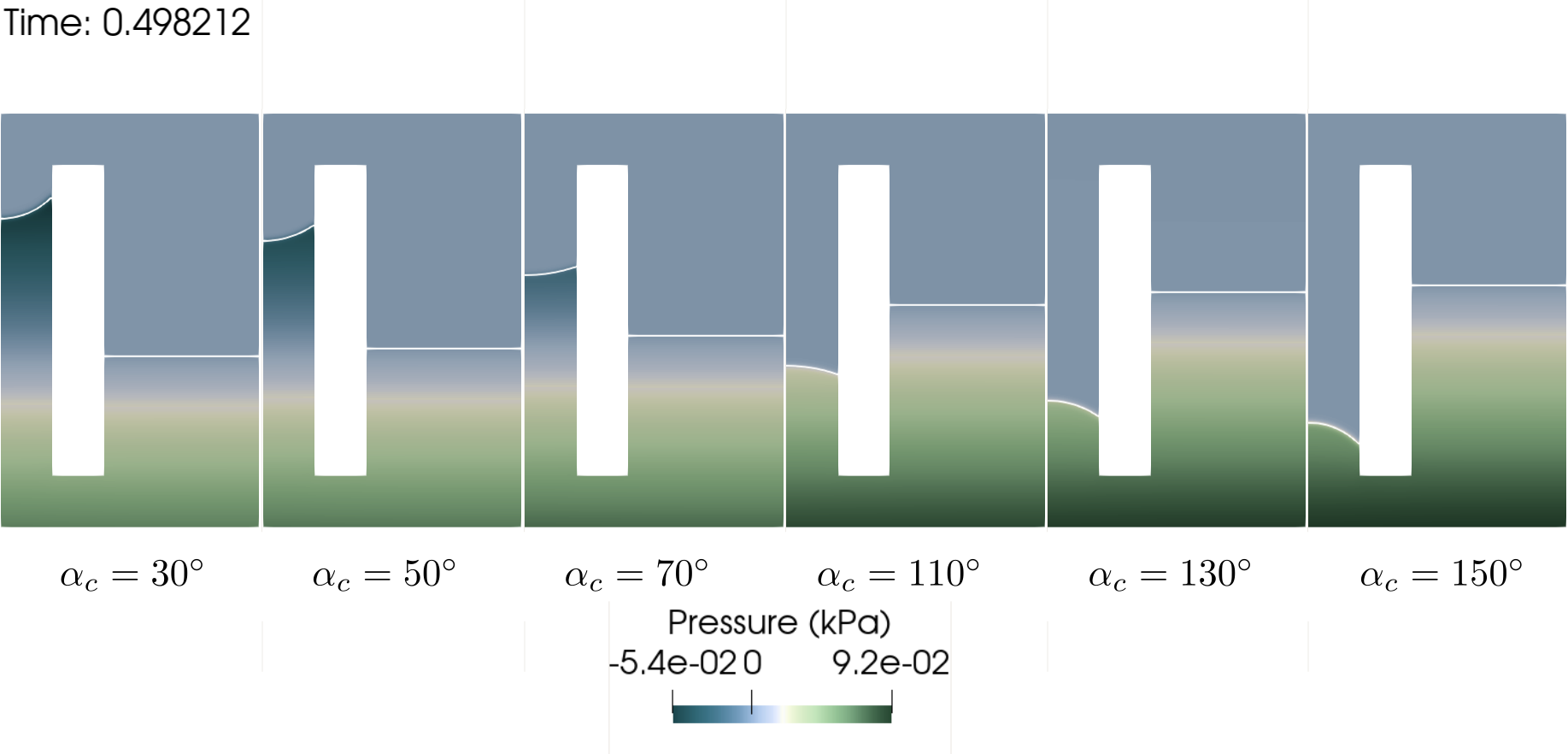
Pressure fields at the end of the simulation for different angles of contact.

Possibilities for Extension

• Going 3D: the mesh can be extruded into the third dimension and there is an adaptation of the Jurin’s law in three dimensions. Some results are available in the literature for comparison (see Lovrić et al. [2])

• Investigate the effect of a no-slip boundary condition: instead of the slip boundary condition imposed on the inner face of the wall, we could try to use a no-slip boundary condition. This situation would be closer to a real capillary rise experiment. We expect to observe a different transient state with this new boundary condition.

References

[1]

S. Liu, S. Li, and J. Liu, ‘Jurin’s law revisited: Exact meniscus shape and column height’, Eur. Phys. J. E, vol. 41, no. 3, p. 46, Mar. 2018, doi: 10.1140/epje/i2018-11648-1.

[2]

A. Lovrić, W. G. Dettmer, and D. Perić, ‘Low Order Finite Element Methods for the Navier-Stokes-Cahn-Hilliard Equations’, Nov. 15, 2019, arXiv: arXiv:1911.06718. doi: 10.48550/arXiv.1911.06718.